Frames
0 ContainersFiles in Frames
Order by

Kleinlogel
Short Description:
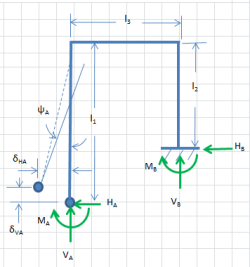
Various frames: rectangular, gable, and skillion, with pinned and fixed bases. Each is set up with...
Submitted By:
Last Modified
11 Apr 2010
Downloads:
297