SageMath Note Book
Description
Sign up for an account here http://www.sagenb.org/ and you can access the knowledge of http://www.sagemath.org/ to solve all your difficult maths problems.
You will find these links helpful too:
Screencasts – videos explain how Sage works
Sage for Newbies – book by T. Kosan
When you have an account you'll be able to view lots of published calculations on http://www.sagenb.org/pub/. If you see the error "It looks like jsMath failed to set up properly (error code -7). I will try to keep going, but it could get ugly.", you haven't installed the TeX fonts which help jsMath render beautiful mathematics. To get the nice TeX display with jsMath, please download a set of fonts from here: http://www.math.union.edu/~dpvc/jsMath/download/jsMath-fonts.html.
This free open source resource offers you the power of a full symbolic maths package like Maple, Mathematica, Matlab, and Magma (which cost $1000 - $2000). The browser text interface makes it easy to copy and paste into your Excel worksheets. I barely scratch the surface in terms of its power but I'll be returning to solve the following types of problem:
Solving Equations
Thesolve function solves equations. To use it, first specify
some variables; then the arguments to solve are an equation (or a
system of equations), together with the variables for which to solve:
sage: x = var('x')
sage: solve(x^2 + 3*x + 2, x)
[x == -2, x == -1]
You can solve equations for one variable in terms of others:
sage: x, b, c = var('x b c')
sage: solve([x^2 + b*x + c == 0],x)
[x == (-sqrt(b^2 - 4*c) - b)/2, x == (sqrt(b^2 - 4*c) - b)/2]
You can also solve for several variables:
sage: x, y = var('x, y')
sage: solve([x+y==6, x-y==4], x, y)
[[x == 5, y == 1]]
Differentiation, Integration, etc.
Sage knows how to differentiate and integrate many functions. For example, to differentiate sin(u) with respect to u, do the following:
sage: u = var('u')
sage: diff(sin(u), u)
cos(u)
To compute the fourth derivative of sin(x2):
sage: diff(sin(x^2), x, 4) 16*x^4*sin(x^2) - 12*sin(x^2) - 48*x^2*cos(x^2)
To compute the partial derivatives of x2 + 17y2 with respect to x and y, respectively:
sage: x, y = var('x,y')
sage: f = x^2 + 17*y^2
sage: f.diff(x)
2*x
sage: f.diff(y)
34*y
Solving Differential Equations
You can use Sage to investigate ordinary differential equations. To solve the equation x'+x-1=0:
sage: t = var('t') # define a variable t
sage: x = function('x',t) # define x to be a function of that variable
sage: DE = lambda y: diff(y,t) + y - 1
sage: desolve(DE(x(t)), [x,t])
'%e^-t*(%e^t+%c)'
This uses Sage's interface to Maxima [Max], and so its output may be
a bit different from other Sage output. In this case, this says that
the general solution to the differential equation is x(t) =
e–t(et
+ c).
You can compute Laplace transforms also; the Laplace transform of t2et - sin(t) is computed as follows:
sage: s = var("s")
sage: t = var("t")
sage: f = t^2*exp(t) - sin(t)
sage: f.laplace(t,s)
2/(s - 1)^3 - 1/(s^2 + 1)
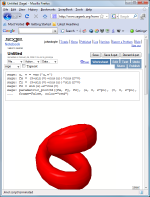
Three-Dimensional Plots
Sage produces three-dimensional plots using an open source package called [Jmol]. E.g. a twisted torus:
sage: u, v = var('u,v')
sage: fx = (3+sin(v)+cos(u))*cos(2*v)
sage: fy = (3+sin(v)+cos(u))*sin(2*v)
sage: fz = sin(u)+2*cos(v)
sage: parametric_plot3d([fx, fy, fz], (u, 0, 2*pi), (v, 0, 2*pi),
... frame=False, color="red")
Calculation Preview
Full download access to any calculation is available to users with a paid or awarded subscription (XLC Pro).
Subscriptions are free to contributors to the site, alternatively they can be purchased.
Click here for information on subscriptions.