Beam Transverse Vibration Mode Shapes - AZ.xls

Purpose of calculation
Calculate and plot the modes shapes of a beam under transverse vibrations.

Calculation Reference
Dynamics and Vibrations, John Wiley & Sons (2008), Table 9.2 (p. 442)

Calculation Validation
Reproduction of a sample calculation from a published calculation reference (on pp. 444 and 447).

Calculation Reference

Dynamics and Vibrations

Vibration Handbook

Structural Dynamics

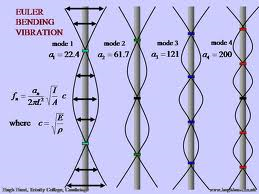
When a beam is subjected to vibration, it can vibrate in different ways, called vibration modes. Each mode corresponds to a specific pattern of deflection of the beam.

The first mode of vibration for a beam is called the fundamental mode. In this mode, the beam deflects in a single hump, either upwards or downwards, with a wavelength equal to twice the length of the beam. This mode has the lowest natural frequency of vibration, and is the most common mode of vibration in everyday structures.

The second mode of vibration is the first overtone mode. In this mode, the beam deflects in two humps, with a wavelength equal to the length of the beam. The two humps are equal in magnitude but opposite in direction.

Subsequent modes of vibration have increasing numbers of humps, and correspond to higher natural frequencies of vibration. For example, the third mode of vibration has three humps, the fourth mode has four humps, and so on.

The shape of each vibration mode depends on the boundary conditions of the beam. For example, a simply supported beam will have different vibration modes than a clamped beam or a beam with one end fixed and the other end free.

Understanding the vibration modes of a beam is important in designing and analyzing structures that are subjected to vibration, such as bridges, buildings, and aerospace structures. By understanding the vibration modes, engineers can design structures that are less susceptible to vibration and that can withstand the stresses caused by vibration.