Eigenvalue Analysis

The goal of modal analysis in structural mechanics is to determine the natural mode shapes and frequencies of an object or structure during free vibration. It is common to use the finite element method (FEM) to perform this analysis because, like other calculations using the FEM, the object being analyzed can have arbitrary shape and the results of the calculations are acceptable. The types of equations which arise from modal analysis are those seen in eigensystems. The physical interpretation of the eigenvalues and eigenvectors which come from solving the system are that they represent the frequencies and corresponding mode shapes. Sometimes, the only desired modes are the lowest frequencies because they can be the most prominent modes at which the object will vibrate, dominating all the higher frequency modes.

Calculation Reference
Eigenvalue

Finite Element Method

Dynamic Analysis

In the context of structural analysis, eigenvalue analysis is used to investigate the dynamic behavior of structures. It helps to determine natural frequencies and mode shapes, which are essential to understanding how a structure responds to different types of dynamic loads, such as earthquakes, wind, or machinery vibrations.

Natural frequencies are the frequencies at which a structure tends to vibrate when it is excited by an external force. They depend on the stiffness and mass distribution of the structure. A structure has multiple natural frequencies, each associated with a specific mode shape.

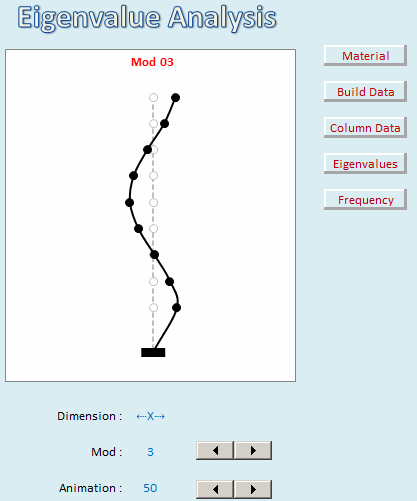
Mode shapes are the characteristic patterns of deformation or displacement that occur when a structure vibrates at a natural frequency. They show how different parts of the structure move relative to each other during vibration.

Eigenvalue analysis in structural analysis typically involves the following steps:

1. Formulate the equations of motion: Start by formulating the governing equations of motion for the structure, usually represented as a second-order differential equation:

M * x''(t) + K * x(t) = F(t)

Where:

• M is the mass matrix
• x''(t) is the acceleration vector
• K is the stiffness matrix
• x(t) is the displacement vector
• F(t) is the external force vector

2. Convert to a standard eigenvalue problem: By assuming a harmonic solution of the form x(t) = φ * e^(iωt), the governing equation can be transformed into a standard eigenvalue problem:

(K - ω^2 * M) * φ = 0

Where:

• ω is the circular natural frequency
• φ is the mode shape (eigenvector)

3. Compute eigenvalues and eigenvectors: Solve the standard eigenvalue problem to obtain the eigenvalues (ω^2) and eigenvectors (φ). The square root of each eigenvalue represents a circular natural frequency of the structure, and the corresponding eigenvector represents the associated mode shape.

4. Interpret the results: Analyze the obtained natural frequencies and mode shapes to understand the dynamic behavior of the structure. This information is crucial for designing structures to withstand dynamic loads and avoid issues such as resonance or excessive vibrations.

It is important to note that eigenvalue analysis provides information about the linear behavior of structures, and for highly nonlinear systems, more advanced techniques like nonlinear dynamic analysis may be required.