RK4 Non-Linear Damped Oscillator — Car Suspension Model

The Engineering Problem

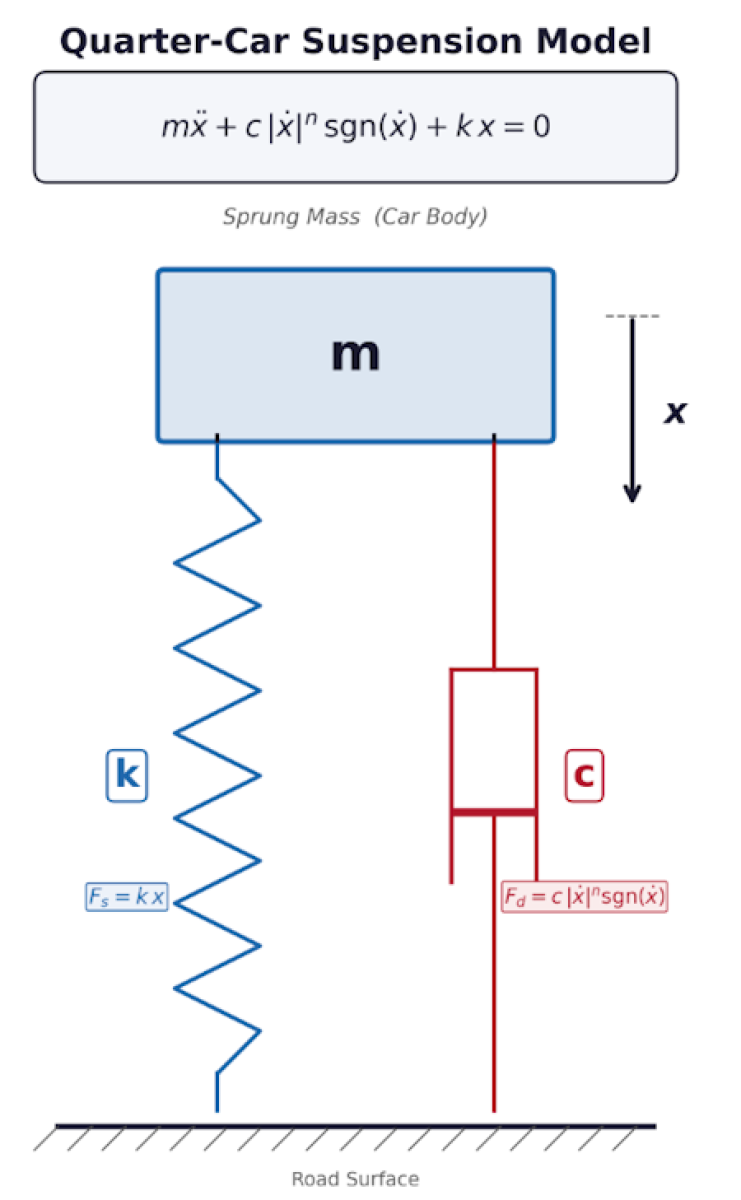
When a car hits a pothole, the suspension must absorb the impact and return the vehicle to a smooth ride. This involves a mass (the car body) connected to the road through a spring (coil spring) and damper (shock absorber). Real shock absorbers exhibit non-linear behaviour — they resist motion more strongly at higher velocities.

This calculation models a quarter-car suspension as a non-linear damped oscillator:

m·x'' + c·|x'|ⁿ·sign(x') + k·x = 0

where n > 1 gives the progressive damping characteristic of real automotive dampers.

The Runge-Kutta 4th Order Method (RK4)

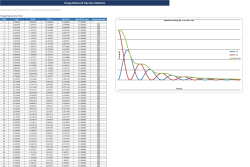
Unlike Euler's Method which uses a single slope estimate per step, RK4 evaluates the slope at four strategically chosen points within each step, then takes a weighted average. This gives dramatically better accuracy — 4th order convergence means halving the step size reduces error by a factor of 16.

The system is converted to two coupled first-order equations:

• y₁' = y₂ (velocity)
• y₂' = (-c·|y₂|ⁿ·sign(y₂) - k·y₁) / m (acceleration)

At each step, four intermediate evaluations (k₁ through k₄) are computed for both equations. All intermediate values are visible in the spreadsheet so the method can be studied and verified.

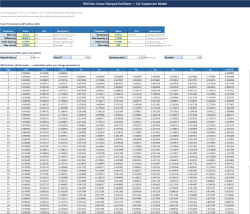
Interactive Parameters

All input parameters (mass, stiffness, damping coefficient, non-linearity exponent, initial conditions, step size) are in clearly marked yellow cells. Change any value and the entire 400-step solution, all charts, and all validation checks recalculate automatically.

What This Calculation Can Be Used For

1. Automotive Suspension Design: Predict oscillation decay, analyse ride comfort, compare damper characteristics
2. Earthquake Engineering: Analyse structural response to ground motion (single-degree-of-freedom approximation)
3. Mechanical Vibration Analysis: Any spring-mass-damper system with non-linear damping
4. Educational: Learn RK4 by examining every intermediate calculation step
5. Method Validation: Built-in energy balance and boundary condition checks demonstrate good engineering practice

Limitations and Considerations

Accuracy:

• RK4 is 4th-order accurate, meaning error decreases as h⁴ — much better than Euler's method
• The default step size (h = 0.005s) gives ~140 steps per oscillation period, providing excellent accuracy
• For critical applications, halve h and compare results to verify convergence

When to Use More Advanced Methods:

• Adaptive step size (RK45): Automatically adjusts h — better for production work
• Implicit methods (BDF, Radau): Required for stiff systems where explicit methods become unstable
• Multi-degree-of-freedom: Real vehicles need models with more masses and springs

Engineering Judgment:

• Always verify results make physical sense — displacement should decay to zero
• Check the natural frequency falls in the expected range (1–2 Hz for passenger cars)
• Verify the damping ratio is reasonable (ζ = 0.2–0.4 for comfortable ride)
• The built-in energy balance check ensures mechanical energy never increases
• Compare with experimental data when available