Simple Harmonic Motion

Purpose of calculation:
Simple Harmonic Motion

Calculation Reference
http://hyperphysics.phy-astr.gsu.edu/hbase/shm.html

Calculation Validation
Reproduction of a sample calculation from a published calculation reference.

Calculation Reference

Simple Harmonic Motion

Dynamics

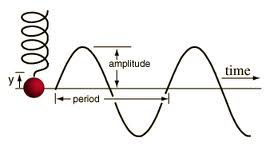
Simple harmonic motion (SHM) is a type of periodic motion where an object moves back and forth along a straight path under the influence of a restoring force that is directly proportional to the displacement from the equilibrium position and acts in the opposite direction of the displacement. This motion is sinusoidal in time, meaning it follows a sine or cosine function.

Examples of simple harmonic motion include the oscillation of a mass attached to a spring or the swinging of a pendulum with small amplitude.

The equation for simple harmonic motion is given by:

x(t) = A * cos(ωt + φ)

where:

• x(t) is the displacement of the object from its equilibrium position as a function of time (t)
• A is the amplitude of the oscillation, which represents the maximum displacement from the equilibrium position
• ω (omega) is the angular frequency of the oscillation, related to the period (T) and frequency (f) by the formulas ω = 2πf = 2π/T
• φ (phi) is the phase angle, which determines the starting point of the motion in the oscillation cycle

The restoring force (F) acting on the object in simple harmonic motion is given by:

F = -k * x(t)

where:

• k is the spring constant or the proportionality constant of the restoring force
• x(t) is the displacement from the equilibrium position at time t

The velocity (v) and acceleration (a) of the object in simple harmonic motion can be derived from the displacement equation:

v(t) = -Aω * sin(ωt + φ) a(t) = -Aω² * cos(ωt + φ)

In simple harmonic motion, the object's acceleration is always directed towards the equilibrium position and is proportional to the displacement from the equilibrium position. The system's potential energy and kinetic energy exchange as the object oscillates, but the total mechanical energy remains constant, provided there is no energy loss due to friction or damping.