Friction Factor Formulas

Friction Factor Formulas, Colebrook Equation Solution Comparisons.

Friction factor formulas are used to calculate the friction factor, a dimensionless parameter that characterizes the resistance to flow in a pipe or channel. The friction factor is an important parameter in fluid mechanics, as it affects the pressure drop and flow rate of the fluid.

The Colebrook equation is a widely used formula for calculating the friction factor in turbulent flow, which is characterized by high Reynolds numbers. The Colebrook equation is an implicit equation that relates the friction factor to the Reynolds number and the relative roughness of the pipe. It is given by:

1/√f = -2 log(ε/D/3.7 + 2.51/Re √f)

where f is the friction factor, ε is the absolute roughness of the pipe, D is the diameter of the pipe, and Re is the Reynolds number.

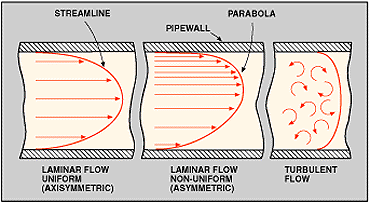
Other friction factor formulas are available for laminar flow, transitional flow, and low-Reynolds-number flow. These formulas include the Hagen-Poiseuille equation, the Blasius equation, and the Darcy-Weisbach equation.

The accuracy and applicability of the various friction factor formulas depend on the flow regime, pipe geometry, and fluid properties. The Colebrook equation is considered to be a highly accurate and widely applicable formula for turbulent flow, but it is computationally intensive and requires iterative solutions. The other friction factor formulas are simpler and easier to use, but they may have limitations in certain flow regimes or pipe geometries.

Comparisons of the Colebrook equation and other friction factor formulas have been conducted in various studies, with mixed results depending on the specific conditions and assumptions. In general, the Colebrook equation is considered to be a reliable and accurate formula for calculating the friction factor in turbulent flow, but the other formulas may be more appropriate for certain applications or simplifications.