Travelling salesman problem
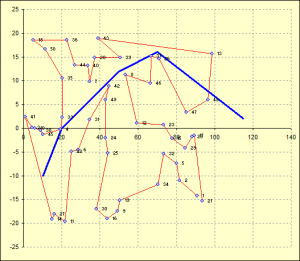
Description
This spreadsheet solves the famous travelling salesman problem of finding the shortest cyclical itinerary for a travelling salesman who must visit each of N cities in turn. In addition a penalty may me assigned for each river crossing. An algorithm is based on the method of simulated annealing published in the Numerical Recipes in C, 2nd edition (1992).
Yakov Polyakov is another 'spreadsheet king' and an ExcelCalcs User. He is very worthy of our praise and has helped me out of a few tight spots in my time with his many superb structural engineering spreadsheets - you'll find a link to his site here.
The Traveling Salesman Problem (TSP) is a classic optimization problem in the field of computer science and operations research. The goal is to find the shortest possible route that visits each city exactly once and returns to the origin city, given a list of cities and the distances between each pair of cities. TSP is an NP-hard problem, meaning that no efficient algorithm is known to solve it exactly for large instances in a reasonable amount of time.
There are various approaches to solving the TSP, including exact algorithms, heuristics, and metaheuristics. For smaller instances, exact algorithms like the Held-Karp algorithm or branch-and-bound can be used. For larger instances, heuristics and metaheuristics such as nearest neighbor, simulated annealing, genetic algorithms, and ant colony optimization can be employed to find good approximate solutions.
Keep in mind that the nearest neighbor algorithm does not guarantee an optimal solution. For small instances, you can use exact algorithms, but for large instances, it's usually better to employ more advanced heuristics or metaheuristics to find good approximate solutions.
Calculation Preview
Full download access to any calculation is available to users with a paid or awarded subscription (XLC Pro).
Subscriptions are free to contributors to the site, alternatively they can be purchased.
Click here for information on subscriptions.

