Area of circular segment.xls

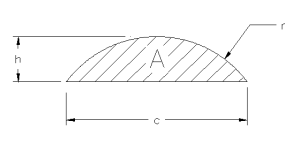
Sometimes it is necessary to find the area of a circular segment when the radius is not directly known. This sheet will compute the radius and resulting segment area when only the chord length and height are given.

Calculation Reference
Geometry

Given the chord length (c) and the height (h) of a circular segment, we can compute the radius (r) and the resulting segment area (A_segment) using the following steps:

1. Calculate the radius (r): We can use the Pythagorean theorem and the properties of an isosceles triangle formed by the chord, radius, and height of the segment.

a. Divide the chord length (c) by 2 to find half the chord length (c/2). b. Use the Pythagorean theorem to find the radius (r):

r = ((c/2)^2 + h^2) / (2*h)

2. Calculate the angle (theta) subtended by the chord at the center of the circle: We can use the sine inverse function to find half the angle (alpha) and then double it to find the full angle (theta).

a. Calculate the sine of half the angle (alpha):

sin(alpha) = (c/2) / r

b. Calculate half the angle (alpha) in radians:

alpha = arcsin(sin(alpha))

c. Calculate the full angle (theta) in radians:

theta = 2 * alpha

3. Calculate the segment area (A_segment): We can use the sector area formula and subtract the area of the triangle formed by the chord, radius, and height of the segment.

a. Calculate the area of the sector (A_sector):

A_sector = (1/2) * r^2 * theta

b. Calculate the area of the triangle (A_triangle):

A_triangle = (1/2) * c * h

c. Calculate the segment area (A_segment):

A_segment = A_sector - A_triangle

Now, you have the radius (r) and the resulting segment area (A_segment) when only the chord length (c) and height (h) are given.