Corrugated plates
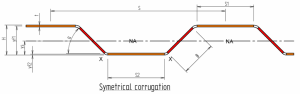
Description
Purpose of calculation
Calculation of section properties of Corrugated Plates
Comments
This calculation sheet is a combination of various formulas from books as noted. The SANS code used is similar to British standards.It is recommended that profile to be drawn in CAD to determine correct dimensions when critical working limits are encountered.
References
Strengths of Material (V Elliot)
Southern African Steel Construction Handbook (Table 13.7)
SANS 0162-2: 1993. The structural uses of steel Part 2: Limit states design of cold formed steelworks
Validation
Corrugation properties is checked by modelling profile with Solid Edge V20 & physical properties function.
Calculation Reference
Strengths of Material Elliot
Southern African Steel Construction Handbook
Limit states design of cold formed steelworks
Calculation Preview
Submitted By:
Submitted On:
12 Nov 2009
File Size:
360.50 Kb
Downloads:
84
File Version:
1.0
This download is for Registered Users Only.
Perhaps you need to login or register.
Thanks.