intersect_circle_line.xls

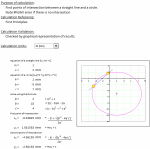
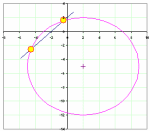
Purpose of calculation: Find points of intersection between a straight line and a circle.
Note #NUM! error if there is no intersection
Calculation Reference: First Principles
Calculation Validation: Checked by graphical representation of results.

Calculation Reference

Geometry

Coordinates

To find the points of intersection between a straight line and a circle, we need to solve the equations of the line and the circle simultaneously.

Let the equation of the line be y = mx + b, where m is the slope and b is the y-intercept. Let the equation of the circle be (x-a)^2 + (y-b)^2 = r^2, where (a,b) is the center of the circle and r is the radius.

Substituting y = mx + b into the equation of the circle, we get:

(x-a)^2 + (mx + b - b)^2 = r^2

Simplifying, we get:

(x-a)^2 + (mx)^2 = r^2

Expanding the squares, we get:

x^2 - 2ax + a^2 + m^2x^2 = r^2

Rearranging, we get:

(m^2 + 1)x^2 - 2ax + (a^2 - r^2) = 0

This is a quadratic equation in x. Solving for x using the quadratic formula, we get:

x = [a ± sqrt(a^2 - (m^2 + 1)(a^2 - r^2))] / (m^2 + 1)

Substituting this value of x into the equation of the line, we get the corresponding values of y:

y = mx + b

So the points of intersection between the line and the circle are:

(x1, y1) = ([a + sqrt(a^2 - (m^2 + 1)(a^2 - r^2))] / (m^2 + 1), m([a + sqrt(a^2 - (m^2 + 1)(a^2 - r^2))] / (m^2 + 1)) + b)

(x2, y2) = ([a - sqrt(a^2 - (m^2 + 1)(a^2 - r^2))] / (m^2 + 1), m([a - sqrt(a^2 - (m^2 + 1)(a^2 - r^2))] / (m^2 + 1)) + b)

These are the two points of intersection between the line and the circle.