Vessels Composed of Surfaces of Revolution

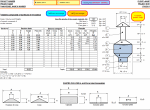
Using the formulae for frustum of a cone, this file computes the volumes, the surfaces and the weights of plates (annular or plain), cylinders, cones and furstum of cones which are generally composing a circular type vessel. An example of the possibilities is given.

Calculation Reference
Volume of Revolution

Tank Design

Geometry

A frustum of a cone is a portion of a cone that remains after a smaller, similar cone is removed from the top by a plane parallel to the base. The formulae to compute the volume, lateral surface area, and total surface area of a frustum of a cone are as follows:

1. Volume (V): To compute the volume of a frustum of a cone, use the formula:

V = (1/3) * π * h * (R1^2 + R2^2 + R1 * R2)

Where: V = volume h = height of the frustum R1 = radius of the larger base R2 = radius of the smaller base

2. Lateral surface area (A_lateral): To compute the lateral surface area of a frustum of a cone, use the formula:

A_lateral = π * (R1 + R2) * L

Where: A_lateral = lateral surface area R1 = radius of the larger base R2 = radius of the smaller base L = slant height of the frustum, which can be calculated using the Pythagorean theorem: L = sqrt(h^2 + (R1 - R2)^2)

3. Total surface area (A_total): To compute the total surface area of a frustum of a cone, which includes the lateral surface area and the areas of the top and bottom bases, use the formula:

A_total = A_lateral + A_top + A_bottom

Where: A_total = total surface area A_lateral = lateral surface area A_top = area of the top base = π * R2^2 A_bottom = area of the bottom base = π * R1^2

For computing the weights of plates (annular or plain), you can use the following formula:

Weight = Volume * Material Density

Where: Weight = weight of the plate Volume = volume of the frustum or plate, calculated using the appropriate formula Material Density = density of the material used for the plate (e.g., steel, aluminum, etc.)

To compute the weights, volumes, and surface areas of frustums and plates, simply apply the corresponding formulae based on the given dimensions and material properties.