Heat transfer by conduction and convection - electrical circuit analogy.xls

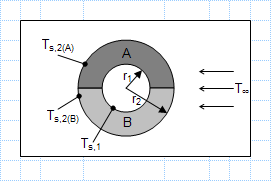
KNOWN: Inner surface temperature of insulation blanket comprised of two semi-cylindrical shells of different materials. Ambient air conditions. Solution by analogy with electrical circuit.

FIND: a) Equivalent thermal circuit.

b) Total heat loss and material outer surface temperature.

ASSUMPTIONS: 1) Steady-state conditions.

2) One-dimensional radial conduction.

3) Infinite contact resistance between materials.

4) Constant properties.

Calculation Reference
Fundamentals of Heat and Mass Transfer - Frank P. Incropera

To solve the heat transfer problem by conduction and convection using an electrical circuit analogy, follow these steps:

a) Equivalent thermal circuit:

1. Identify the layers: Determine the two different materials comprising the insulation blanket's semi-cylindrical shells. Let's label them Material 1 and Material 2.

2. Determine the thermal resistances: Assign thermal resistances to each material layer based on the one-dimensional radial conduction assumption. The thermal resistance (R) of each material can be calculated as:

   R = ln(r2/r1) / (2πkL)

   Where r2 and r1 are the outer and inner radii of the layer, k is the thermal conductivity of the material, and L is the thickness of the layer.

3. Determine the convection resistance: Account for convection heat transfer at the inner and outer surfaces of the insulation blanket. Assign a convection resistance (Rc) for each surface using the convection heat transfer coefficient (h):

   Rc = 1 / (hA)

   Where h is the convection coefficient and A is the surface area.

4. Construct the thermal circuit: Represent the thermal resistances as resistors and the convection resistances as conductances. Connect these elements in series, starting with the innermost surface of the insulation blanket.

b) Total heat loss and material outer surface temperature:

1. Determine the boundary conditions: Identify the inner surface temperature of the insulation blanket, the ambient air temperature, and the convection coefficients associated with the inner and outer surfaces.

2. Apply the electrical analogy: Treat the thermal circuit as an electrical circuit and apply Ohm's Law. The total heat loss (Q) can be calculated as the product of the current (I) flowing through the circuit and the voltage drop (ΔV) across the circuit:

   Q = I * ΔV

   Where I represents the heat transfer rate (in watts) and ΔV represents the temperature difference between the inner surface and the ambient air.

3. Solve for the total heat loss: The total heat loss can be calculated using the electrical analogy, taking into account the resistances and conductances of the thermal circuit.

4. Calculate the material outer surface temperature: Once the total heat loss is known, use the boundary conditions and the thermal circuit to determine the outer surface temperature of the material.

By representing the problem as an equivalent thermal circuit and applying the electrical circuit analogy, you can determine the total heat loss and the outer surface temperature of the material in the insulation blanket.