Heat transfer in cooling fins.xls
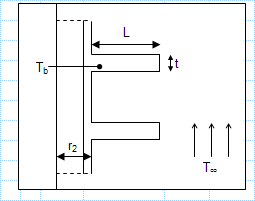
Description
KNOWN: Dimensions and base temperature of aluminum fins of rectangular profile. Ambient air conditions.
FIND: a) Fin efficiency and effectiveness.
b) Rate of heat transfer per unit length of tube.
ASSUMPTIONS: 1) Steady-state conditions.
2) One-dimensional radial conduction in fins .
3) Constant properties.
4) Negligible Radiation.
5) Negligible base contract resistance.
6) Uniform convection coefficient.
Calculation Reference
Fundamentals of Heat and Mass Transfer - Frank P. Incropera
To determine the heat transfer coefficient between a sphere and an air stream, we can use the method of lumped capacitance analysis. This approach assumes that the temperature of the sphere is spatially uniform and that radiation exchange effects are negligible. Here's how you can proceed:
-
Obtain temperature-time data: Obtain the temperature-time history of the copper sphere as it is exposed to the air stream. Ideally, this data should cover a significant portion of the cooling process.
-
Determine the initial and ambient temperatures: Identify the initial temperature of the sphere (T_initial) and the ambient temperature of the air stream (T_ambient). These temperatures should be measured or known.
-
Calculate the Biot number: The Biot number (Bi) is a dimensionless parameter that characterizes the relative importance of convection and conduction in the heat transfer process. It can be calculated using the following equation:
Bi = h * R / k
Where h is the heat transfer coefficient, R is the characteristic length of the sphere (typically its radius), and k is the thermal conductivity of the sphere material (copper in this case).
-
Determine the time constant: The time constant (τ) represents the time it takes for the sphere to cool to a significant extent. It can be calculated using the following equation:
τ = (ρ * V * c) / (h * A)
Where ρ is the density of the sphere material, V is the volume of the sphere, c is the specific heat capacity of the sphere material, h is the heat transfer coefficient, and A is the surface area of the sphere.
-
Analyze the temperature-time data: Plot the temperature-time data for the cooling process of the sphere. Identify the time at which the temperature reaches a specified fraction (e.g., 0.1 or 0.2) of the initial-ambient temperature difference (T_initial - T_ambient).
-
Determine the heat transfer coefficient: Using the Biot number and the time constant, you can determine the heat transfer coefficient (h) using empirical correlations or analytical solutions specific to the cooling process of a sphere in an air stream.
Note: The specific correlations or solutions used to determine the heat transfer coefficient depend on the specific conditions and geometry of the system. Consult heat transfer literature or relevant resources to identify suitable correlations for your particular case.
By analyzing the temperature-time data and applying the lumped capacitance analysis method, you can estimate the heat transfer coefficient between the sphere and the air stream.
Calculation Preview
Full download access to any calculation is available to users with a paid or awarded subscription (XLC Pro).
Subscriptions are free to contributors to the site, alternatively they can be purchased.
Click here for information on subscriptions.

