Simple 1D conduction.xls

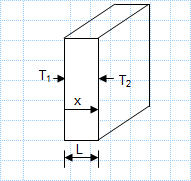
Known: Heat rate, q, through one-dimensional wall of area A, thickness L,thermal conductivity k and inner temperature, T1.
Find: The outer temperature of the wall, T2
Calculation Reference
Harris' Shock and Vibration Handbook

To find the outer temperature of a one-dimensional wall, given the heat rate (q), area (A), thickness (L), thermal conductivity (k), and inner temperature (T1), you can use Fourier's Law of heat conduction. The formula for Fourier's Law in one dimension is:

q = -k * A * (dT/dx)

Where q is the heat rate, A is the area, k is the thermal conductivity, dT/dx is the temperature gradient, and the negative sign indicates heat flowing from the higher temperature side (inner surface) to the lower temperature side (outer surface).

Assuming that the temperature gradient (dT/dx) is constant and the wall is uniform, you can rearrange the equation as follows:

dT/dx = -q / (k * A)

Now, integrate the temperature gradient with respect to x (the distance from the inner surface) from 0 to L:

∫ dT/dx dx = -∫ q / (k * A) dx

(T2 - T1) = - (q / (k * A)) * x

(T2 - T1) = - (q * L) / (k * A)

Finally, rearrange the equation to solve for the outer temperature (T2):

T2 = T1 - (q * L) / (k * A)

Using this equation, you can calculate the outer temperature (T2) of the one-dimensional wall based on the given heat rate, area, thickness, thermal conductivity, and inner temperature.