Base Tangent Length Calculation for Helical Gears

Title: BASE TANGENT LENGTH CALCULATION FOR HELICAL GEAR.

Application of guideline Base tangent length required for gear tooth inspection

Introduction: Base tangent length  (Wk)  is generallly used to determine gear tooth thickness by measuring length across a certain no. of teeth (k) and unit correction factor.

To determine optimum no.of teeth there is two methods-

1. It can be determined by refering to graph in CMTI  handbook pg 268 'Optimum number of teeth'
   
   
   
2. From following calculation method
   
   NOTE : Compulsory follow both method for verification of optimum no. of teeth
   

Calculation Reference

Gear Design

CMTI handbook

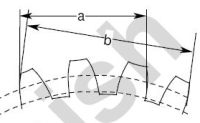
The base tangent length, also known as the span measurement, is an essential parameter for the accurate manufacturing and inspection of helical gears. The base tangent length is the distance between two points on the base circle where the tangent to the base circle is parallel to the tooth profile at the pitch point. This measurement is used to determine the tooth thickness and evaluate the accuracy of the tooth profile.

To calculate the base tangent length (Wt) for helical gears, you can use the following formula:

Wt = π * D * m * cos(β) / Z

where:

• Wt is the base tangent length (span measurement)
• D is the pitch diameter of the gear
• m is the module of the gear (the ratio of pitch diameter to the number of teeth)
• β is the helix angle (the angle between the helix and an axial line on the gear)
• Z is the number of teeth on the gear

In the case of an involute gear profile, it is important to note that the base tangent length calculated using this formula is an approximation, as the true base tangent length is influenced by the shape of the involute curve. However, the approximation is generally accurate enough for most practical purposes.

Remember to use consistent units when performing the calculation (e.g., millimeters or inches for dimensions). Also, make sure to convert the helix angle (β) to radians if your calculator uses radians for trigonometric functions.