Epicyclic Gear Ratios

Epicylic Gears - Ratio Calculation.
Purpose of Calculation - To calculate the ratios of various epicylic gear arrangements.

Calculation Reference - Roymech.co.uk.
https://roymech.co.uk/Useful_Tables/Drive/Epi_cyclic_gears.html

Calculation Validation - On my webpage as identified above I have illustrated three methods of obtaining the required ratios. I have also checked the ratios against Machinery's Handbook 27th edition page 2115.

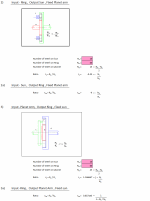
Introduction - An epicylic gear is a planetary gear arrangement consisting of one or more planet (epicyclic) gears (P) meshed and rotating round a central sun gear (S).   The planet gears are also meshed and rotate within an internal ring gear (A).   The planet gears are fixed to a planet carrier-crank arm ( L ) designed to rotate on the same centre as the sun gear.  Only one planet-carrier /crank arm is used in a single epicyclic gear train.   This complicated arrangement (see below) has a number of modes of operation depending on which members are locked.  Epicyclic gears can be based on spur gears, helical gears, or bevel gears.

Calculation Reference
Machinery's Handbook

Machine Design

Epicyclic gears, also known as planetary gears, are gear systems that consist of one or more outer gears (planet gears) rotating around a central gear (sun gear). They are used in various applications, including automatic transmissions, differential drives, and clock mechanisms, due to their compact design and ability to achieve high gear ratios.

To calculate the gear ratios of an epicyclic gear arrangement, it is important to understand the configuration of the gears and their tooth counts. The following steps can be used to calculate the gear ratios:

1. Identify the tooth counts of the gears: Determine the number of teeth for the sun gear (Ns), the planet gears (Np), and the ring gear (Nr). The ring gear is the outer gear that encloses the planet gears and typically has internal teeth.

2. Calculate the gear ratios between the sun and planet gears, and the planet and ring gears: Calculate the ratios between the sun and planet gears (Rs_p) and between the planet and ring gears (Rp_r).

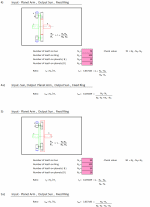
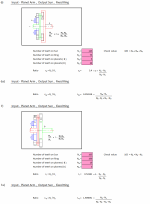
Rs_p = Np / Ns Rp_r = Nr / Np

3. Determine the epicyclic gear arrangement: Depending on the gear configuration, there are three common types of epicyclic gear arrangements:

a) Single-stage planetary gear (one sun, multiple planets, and one ring gear) b) Compound planetary gear (multiple suns and rings connected by planet gears) c) Multi-stage planetary gear (multiple single-stage planetary gears connected in series)

4. Calculate the gear ratios for the epicyclic gear arrangement:

a) For a single-stage planetary gear:

Gear ratio (GR) = (Nr + Ns) / Ns (when the ring gear is fixed)

or

Gear ratio (GR) = Nr / (Ns + Np) (when the sun gear is fixed)

b) For a compound planetary gear:

Calculate the gear ratio for each pair of connected sun and ring gears using the single-stage planetary gear formula, and then multiply the gear ratios together.

c) For a multi-stage planetary gear:

Calculate the gear ratio for each single-stage planetary gear, and then multiply the gear ratios together.

By following these steps, you can calculate the gear ratios of various epicyclic gear arrangements based on their configuration and tooth counts.