involute coords.xls

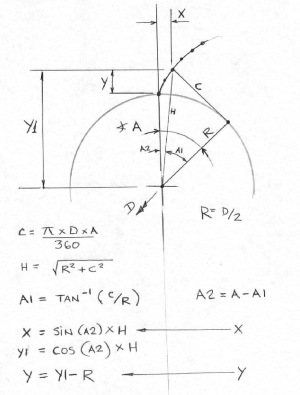
Calculates the XY coordinates along an involute.

Calculation Reference

Machine Design

Gear involute chords refer to straight lines or segments that approximate the involute curve on a gear tooth's profile. The involute curve is the path traced by a point on a straight line (called the 'tangent') as it rolls without slipping along the circumference of the base circle of the gear.

The involute curve is essential in gear design because it provides constant velocity transmission and uniform distribution of load along the contact line between the meshing teeth. However, mathematically defining the curve can be complicated, and working with chords offers a simpler way to approximate the shape of the involute profile.

By dividing the involute curve into small segments (chords), the gear tooth's profile can be represented by a series of straight lines connecting these segments. This simplification makes it easier to work with gear geometry in computer-aided design (CAD) and manufacturing (CAM) systems, as well as in physical measurements and inspection processes.

It is important to note that as the number of chords increases, the approximation of the involute curve becomes more accurate. However, using too many chords can lead to increased complexity in design and manufacturing processes. Therefore, an appropriate balance between the accuracy of the approximation and the simplicity of the representation must be found, depending on the specific application and required precision.

To calculate the XY coordinates along an involute, you'll need the base diameter (Db) of the gear and the pressure angle (φ). Here's a step-by-step guide:

1. Required input parameters:

• Base diameter (Db): The diameter of the circle from which the involute curve starts.
• Pressure angle (φ): The angle between the line of action and the line tangent to the pitch circle at the point of tooth engagement.
• Number of points (n): The number of points along the involute curve you want to calculate.

2. Calculate the radius of the base circle (Rb): Rb = Db / 2

3. Calculate the involute angle increment (Δθ): Δθ = (2 * π) / n

4. Calculate the XY coordinates for each point along the involute curve: For each point i (from 0 to n), calculate the involute angle (θi) and the rolling angle (αi) using the following formulas:

θi = i * Δθ αi = θi - tan(θi) + tan(φ) * (1 - cos(θi))

Now, calculate the XY coordinates (xi, yi) for each point i along the involute curve using the following formulas:

xi = Rb * (cos(αi) + (θi - sin(θi)) * sin(αi)) yi = Rb * (sin(αi) - (θi - sin(θi)) * cos(αi))

These formulas will help you calculate the XY coordinates along an involute gear curve. Note that the number of points (n) should be chosen to provide an adequate resolution of the involute curve, depending on your specific application.