Loading Calculation Sheet.xlsx
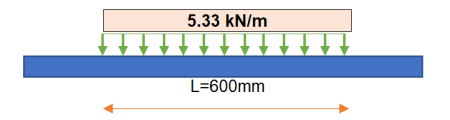
Description
Beam bending theory is a fundamental concept in structural engineering and solid mechanics that deals with the deformation and stress distribution in beams subjected to external loads. It is based on several key principles and assumptions, which can be summarised as follows:
-
Euler-Bernoulli Beam Theory: This theory assumes that the beam is slender, homogeneous, and isotropic, with a linear stress-strain relationship. It states that plane cross-sections perpendicular to the beam's neutral axis remain plane and perpendicular after bending.
-
Neutral Axis: The neutral axis is an imaginary line within the beam's cross-section where no elongation or contraction occurs during bending. This line is the centroid of the cross-sectional area of the beam.
-
Bending Moment: The bending moment (M) is the algebraic sum of moments acting on a cross-section of the beam. It quantifies the beam's tendency to bend due to the applied loads.
-
Shear Force: The shear force (V) is the algebraic sum of vertical forces acting on a beam section. It quantifies the beam's tendency to shear, or slide, due to the applied loads.
-
Bending Stress: The bending stress (σ) is the internal resistance to bending in the beam's material. It can be calculated using the flexure formula: σ = (M*c)/I, where M is the bending moment, c is the distance from the neutral axis to the point of interest, and I is the moment of inertia of the beam's cross-section.
-
Deflection: The deflection (δ) is the displacement of the beam from its original position due to the applied loads. It can be determined using the beam deflection equations, which are derived from the integration of the curvature equation.
-
Boundary Conditions: To solve for the deflection and reaction forces in a beam, appropriate boundary conditions, such as support types (fixed, pinned, or roller) and load types (point, distributed, or moment), must be considered.
-
Superposition Principle: The superposition principle states that the total response of a linear system subjected to multiple loads is the sum of the responses due to each load acting independently. This principle can be used to analyze beams with complex loading conditions.
Beam bending theory is essential in the design and analysis of structures, as it helps engineers predict and control the behavior of beams under various loading conditions, ensuring their structural integrity and safety.
Calculation Preview
Full download access to any calculation is available to users with a paid or awarded subscription (XLC Pro).
Subscriptions are free to contributors to the site, alternatively they can be purchased.
Click here for information on subscriptions.



