RECTBEAM (318-05)

"RECTBEAM" is a spreadsheet program written in MS-Excel for the purpose of analysis/design of rectangular beam or column sections.  Specifically, the ultimate moment capacity, bar spacing for crack control, moments of inertia for deflection, beam shear and torsion requirements, and member capacity for flexure (uniaxial and biaxial) with axial load are calculated.  There is also a worksheet which contains reinforcing bar data tables.
This version is based on the ACI 318-05 Code.

This program is a workbook consisting of ten (10) worksheets, described as follows:


Doc - This documentation sheet
Complete Analysis - Beam flexure, shear, crack control, and inertia
Flexure - Ultimate moment capacity of singly or doubly reinforced beams/sections
Crack Control - Crack control - distribution of flexural reinforcing
Shear - Beam or one-way type shear
Torsion - Beam torsion and shear
Inertia - Moments of inertia of singly or doubly reinforced beams/sections
Uniaxial - Combined uniaxial flexure and axial load
Biaxial - Combined biaxial flexure and axial load
Rebar Data - Reinforcing bar data tables

Program Assumptions and Limitations:

1.  This program follows the procedures and guidelines of the ACI 318-05 Building Code.
2.  This program utilizes the following references:
      a. "Design of Reinforced Concrete - ACI318-05 Code Edition", by Jack C. McCormac (7th Ed.)
      b. "Notes of the ACI318-05 Building Code Requirements for Structural Concrete", by PCA
3.  The "Complete Analysis" worksheet combines the analyses performed by four (4) of the individual worksheets all into one.  This includes member flexural moment capacity, as well as shear, crack control, and inertia calculations.  Thus, any items below pertaining to any of the similar individual worksheets included in this one are also applicable here.
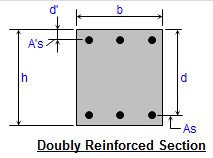
4.  In the "Flexure", "Uniaxial", and "Biaxial" worksheets, when the calculated distance to the neutral axis, 'c', is less than the distance to the reinforcement nearest the compression face, the program will ignore that reinforcing and calculate the ultimate moment capacity based on an assumed singly-reinforced section.
5.  In the "Uniaxial" and "Biaxial" worksheets, the CRSI "Universal Column Formulas" are used by this program to determine Points #1 through #7 of the 10 point interaction curve.  For the most part, these formulas yield close, yet approximate results.  However, these results should be accurate enough for most applications and situations.
6. To account for the fact that the CRSI "Universal Column Formulas" originally utilized f =0.70 for compression, which was applicable up through the ACI 318-99 Code, they have been factored by (0.65/0.70) to account for the reduction in the factor f = 0.65 for compression beginning with ACI 318-02 Code and continuing with the ACI 318-05 Code.  This modification has been made to the equations applicable to Points #1 through #7.
7.  In the "Uniaxial" and "Biaxial" worksheets, the CRSI "Universal Column Formulas", which are used by this program, assume the use of the reinforcing yield strength, fy =60 ksi.
8.  In the "Uniaxial" and "Biaxial" worksheets, this program assumes a "short", non-slender rectangular column with symmetrically arranged and sized bars.
9.  In the "Uniaxial" and "Biaxial" worksheets, for cases with axial load only (compression or tension) and no moment(s) the program calculates total reinforcing area as follows:
           Ast = (NtbAbt) + (NsbAbs) ,  where: Abt and Abs = area of one top/bottom and side bar respectively.
10. In the "Uniaxial" and "Biaxial" worksheets, for pure moment capacity with no axial load, the program assumes bars in 2 outside faces parallel to axis of bending plus 50% of the total area of the side bars divided equally by and added to the 2 outside faces, and program calculates reinforcing areas as follows:
           for X-axis:  As = A's = ((NtbAbt) + (0.50NsbAbs))/2
           for Y-axis:  As = A's = ((NsbAsb+4Atb) + (0.50(Ntb-4)Atb))/2
11. In the "Uniaxial" and "Biaxial" worksheets, for Point #8 (fPn = 0.1f'cAg) on the interaction curve the corresponding value of fMn is determined from interpolation between the moment values at Point #7  (balanced condition, f = 0.65) and Point #9 (pure flexure, f <= 0.90).
12. In the "Complete Analysis" and "Flexure" worksheets as well as the "Uniaxial" and "Biaxial" worksheets (for Point #9, pure flexure) the program first determines the strain in tension reinforcing (et), then the capacity reduction factor (f),and finally ultimate moment capacity (fMn) based on actual input reinforcing.
          a. For et >= 0.005 ("tension-controlled" section): f = 0.90.
          b. For fy/Es < et < 0.005 ("transition" section): f =  0.65+0.25(et-fy/Es)/(0.005-fy/Es) < 0.90   (Es=29000 ksi)
          c. For et <= fy/Es ("compression-controlled" section): f = 0.65
      Note: the ACI 318-05 Code requires that the strain in the tension reinforcing (et) >= 0.004 for both singly and doubly reinforced sections.
13. In the "Uniaxial" and "Biaxial" worksheets, design capacities, fPn and fMn, at design eccentricity,  e = Mu12/Pu, are determined from interpolation within the interaction curve for the applicable axis.
14. In the "Biaxial" worksheet, the biaxial capacity is determined by the following approximations:
          a. For Pu >= 0.1f'cAg, use Bresler Reciprocal Load equation:
              1/fPn = 1/fPnx + 1/fPny - 1/fPo
              Biaxial interaction stress ratio, S.R. = Pu/fPn <= 1
          b. For Pu < 0.1f'c*Ag, use Bresler Load Contour interaction equation:
              Biaxial interaction stress ratio, S.R. = (Mux/fMnx)^1.15 + (Muy/fMny)^1.15 <= 1
15. The "Rebar Data"  worksheet contains tables of reinforcing bar data which include various bar properties, reinforcing bar areas based on spacing, and various plain welded wire fabric properties.
16. This program contains numerous “comment boxes” which contain a wide variety of information including explanations of input or output items, equations used, data tables, etc.  (Note:  presence of a “comment box” is denoted by a “red triangle” in the upper right-hand corner of a cell.  Merely move the mouse pointer to the desired cell to view the contents of that particular "comment box".)

Calculation Reference
ACI 318-05