Strain Calculator from Strain Gauges

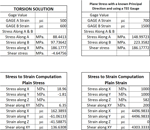
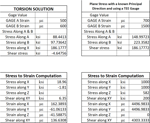
A calculator to convert strain gauge readings in various configuration to equivalent stress.

                                                                       <p>Strain gauge readings provide information on the deformation experienced by a material or structure under applied loads. To convert these readings to equivalent stress, a series of calculations and consideration of the strain gauge configuration are necessary. Here's a summary of the process:</p>

1. Raw strain gauge readings: Obtain the raw strain gauge readings from the sensors installed on the structure or material. These readings may be in microstrain (με) units, which represent the ratio of deformation to the original length.

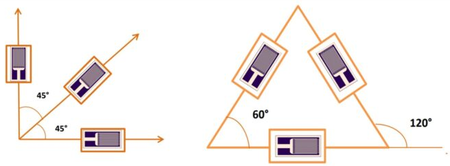
2. Strain gauge configuration: Identify the strain gauge configuration used for the measurements, such as uniaxial, biaxial (90-degree or 45-degree rosette), or triaxial (60-degree delta or 120-degree rectangular rosette). The configuration will determine the calculations required for converting the readings to equivalent stress.

3. Correction factors: Apply any necessary correction factors to the raw strain gauge readings, accounting for factors like temperature changes, gauge factor variations, and zero drifts.

4. Principal strains: For biaxial or triaxial strain gauge configurations, calculate the principal strains (ε1 and ε2) using the corrected strain gauge readings and the equations specific to the configuration. For instance, for a 45-degree biaxial rosette:

   ε1 = (εA + εC) / 2 + √[((εA - εC) / 2)^2 + εB^2] ε2 = (εA + εC) / 2 - √[((εA - εC) / 2)^2 + εB^2]

   Where εA, εB, and εC are the corrected readings from the strain gauges.

5. Material properties: Determine the material properties, such as the elastic modulus (E) and Poisson's ratio (ν), which are necessary for converting strains to stresses.

6. Stress calculations: Calculate the equivalent stress using the principal strains and material properties. For linear elastic materials, the stress-strain relationship can be expressed as:

   σ1 = E * (ε1 - ν * ε2) / (1 - ν^2) σ2 = E * (ε2 - ν * ε1) / (1 - ν^2)

   Where σ1 and σ2 are the principal stresses.

7. Von Mises stress: For a more general stress indicator, especially in ductile materials, calculate the Von Mises stress (σ_VM) using the principal stresses:

   σ_VM = √[0.5 * ((σ1 - σ2)^2 + (σ1 - σ3)^2 + (σ2 - σ3)^2)]

   Where σ3 is the third principal stress, which is zero for plane stress conditions.

After completing these calculations, the equivalent stress values can be used for further analysis, such as assessing structural performance, identifying potential failure points, or validating numerical models.