Tank Liquid Jet Trajectory

Engineering Principle Explanation

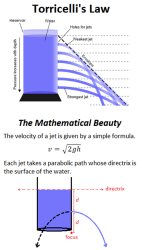
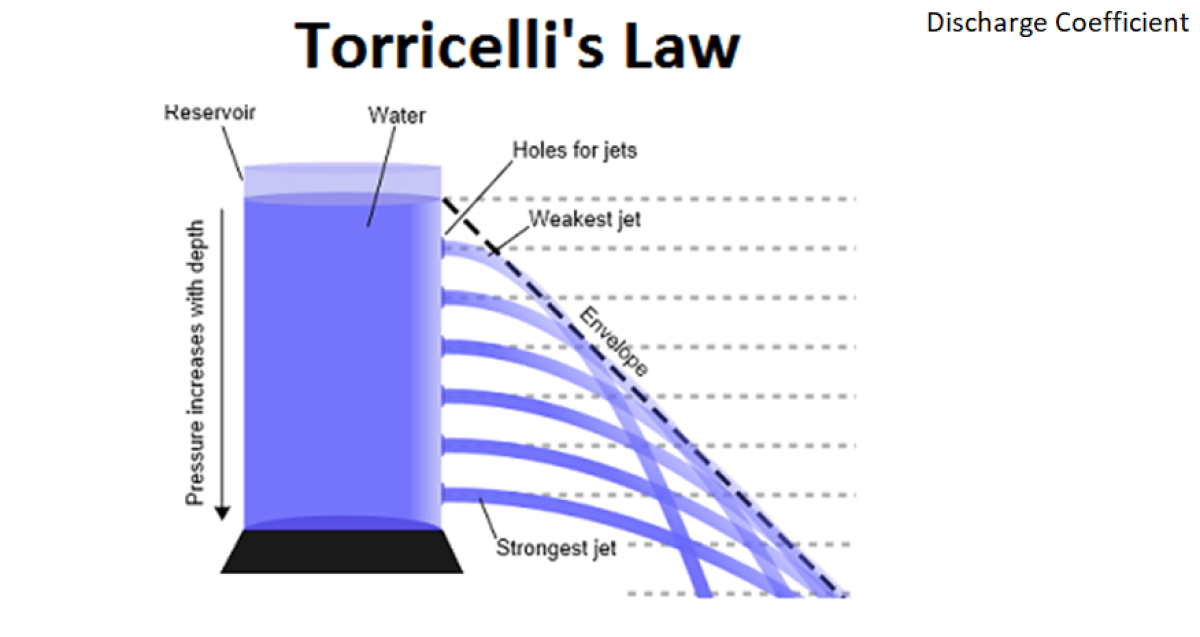
This calculation applies Torricelli's theorem combined with projectile motion physics to predict the trajectory path of liquid discharged from a tank opening. The fundamental principle combines fluid dynamics with classical mechanics to determine where a horizontal jet of liquid will land at various distances from the tank.

Key Engineering Principles:

1. Torricelli's Law: The velocity of liquid flowing from an orifice depends on the height of liquid above the opening, following the relationship V = √(2gh). This is modified by a discharge coefficient to account for real-world losses.

2. Projectile Motion: Once the liquid exits horizontally, it follows a parabolic path governed by the projectile motion equation: y = h + x × tan(α) - g × x² / (2 × V₀² × cos²(α)). For horizontal discharge, the angle α = 0.

3. Discharge Coefficient: The 0.65 value accounts for energy losses due to friction and vena contracta (jet contraction) at the orifice. This reduces the theoretical velocity to a more realistic value.

4. Varying Velocity Profile: As the tank drains, the liquid height decreases, causing the exit velocity to reduce. This creates different trajectory paths at different liquid levels.

5. Combined Analysis: The calculation tracks the jet's vertical position (elevation) at various horizontal distances, showing how the trajectory changes as the tank empties.

Repository Description

Title: Tank Liquid Jet Trajectory Calculator

Description: This Excel calculation tool predicts the trajectory path of liquid jets discharged horizontally from tank openings at various liquid levels. Based on Torricelli's theorem and projectile motion equations, it calculates where the liquid stream will land at different distances from the tank.

Key Features:

• Calculates exit velocity based on liquid height using Torricelli's law
• Applies discharge coefficient (0.65) for realistic flow conditions
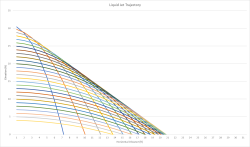
• Computes trajectory paths at multiple liquid levels (31 ft down to 4 ft)
• Determines vertical elevation of jet at horizontal distances from 1 to 15 feet
• Shows how trajectory changes as tank drains

Applications:

• Tank overflow design and splash zone prediction
• Emergency discharge planning
• Irrigation system design
• Industrial process liquid handling
• Fountain and water feature design
• Tank farm layout planning
• Environmental spill containment design

Technical Basis: The calculation combines:

• Torricelli's theorem: V = Cd × √(2gh)
• Horizontal projectile motion: y = y₀ - (g × x²)/(2 × V²)
• Where Cd = discharge coefficient, g = gravitational acceleration, h = liquid height above opening

Input Requirements:

• Tank height (32 ft in example)
• Discharge coefficient (0.65 typical)
• Horizontal distances of interest

Output Results:

• Exit velocity at each liquid level
• Trajectory elevation at distances from 1-15 feet
• Complete trajectory mapping as tank drains
• Visual representation of jet paths at different fill levels

This tool is essential for engineers designing tank systems, spillways, or any application where liquid discharge trajectories must be predicted for safety, environmental protection, or process design purposes.