Pin and Lug - Static and Fatigue.xls

Purpose of calculation:
Calculate the proof and ultimate strength of obliquely loaded lugs.
Calculate the fatigue strength of lug.
This is an extension of a simpler calculation which only considers static strength.
Calculation Reference
Traditional UK railway method.
A.P.T. Mechanical Design Note No APT/MD 257
Strength of Lugs in Fatigue by R. B Heywood
Stress, Strain and Strength by R. C. Juvinall
Calculation Validation
This calculation requires validation.
Design Tips
It is normal to choose a pin size 6mm larger than required to allow for off centre drilling etc.
You may want to consider the use of a replaceable bush to increase the wear life of the lug.
You may also have to consider fatigue life.
Pin bending stresses also needs consideration but is not covered in the calculation below.
Design Procedure
================
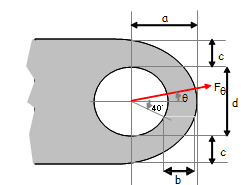
Lug Dimensions
Material selection
Applied Loads
+ve. force loads the eye of the lug.
-ve. force is compressive.
Minimum force applied to the lug
Minimum force applied to the lug
Number of cycles applied
Orientation of applied force
Summary
Proof strength check.
Ultimate strength check.
Fatigue strength check.
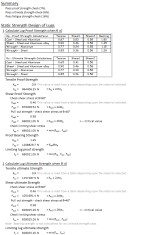
Static Strength Design of Lugs
==============================
1 Calculate Lug Proof Strength when ?=0
Tensile Proof Strength
Shear Proof Strength
Check shear stress at ?=90°
Pull out strength - check shear stress at ?=40°
Check limiting shear stress
Proof Bearing Strength
Limiting lug proof strength
2) Calculate Lug Ultimate Strength when ?=0
Tensile ultimate Strength
Shear ultimate Strength
Check shear stress at ?=90°
Pull out strength - check shear stress at ?=40°
Check limiting shear stress
Note - Bearing strength is not considered for an ultimate strength case.
Limiting lug ultimate strength
3) Calculate Lug Strength for Oblique or Transversely Loaded Lugs
4) Static Strength Pass/Fail Criteria
Proof demand to capacity ratio
Ultimate demand to capacity ratio
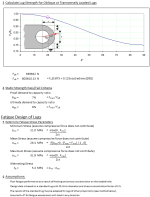
Fatigue Design of Lugs
======================
5) Determine Fatigue Stress Parameters
Minimum Stress (assume compressive force does not contribute)
Mean Stress (assume compressive force does not contribute)
Maximum Stress (assume compressive force does not contribute)
Alternating Stress
6) Assumptions:
Poor fatigue performance as a result of fretting and stress concentration on the loaded hole.
Design data is based on a standard lug with 25.4mm diameter and stress concentration factor of 2.5.
The results of the standard lug may be adapted for lugs of other proportions (see method below).
Assume ? = 0° for fatigue assessment with load in any direction.
7) Determine stress concentration factor, KE
8) Determine size factor, KS
Change units of d into mm for size factor lookup.
9) Determine thickness ratio correction factor, CT
10) Determine casting factor, CF
11) Read Heywood's Lug Fatigue Curve.
12) Fatigue Pass/Fail Criteria
Allowable alternating stress

Calculation Reference
Machine Design
Bruhn Design of aircraft
Heywood Design of Lugs