Lift Lug calc for Skid

PLEASE NOTE: "Lift Lug calc for Skid" has links with "Weight & Bolting_lse.xls" These may be downloaded separately or together as a zip file.
LIFTING LUG DESIGN CALCULATION (SKID)     
     
ITEM  : C.I. SKID (A-6810)     
PROJECT NO. C.I Injection system (A-6810) - Permas Field Substructure    
     
     
Weight of component to be lifted      
Component force acting on beam, F     
Impact factor     
     
SKID LUG SIZING     
 
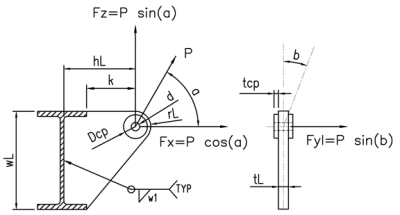
Distance from lug hole to edge of beam, k     
Lug radius, rL     
Lug thickness, tL     
Lug base width, wL     
Diameter of hole, d     
Distance from lug hole to base, hL     
Collar plate thickness, tcp     
Collar ring diameter, Dcp     
     
  Clearance btw shackle & lug size   
     
    Lug thickness, tL
  A = 42.9 mm  40
     
    Lug radius, rL
  C = 95.5 mm 70
     
  Since A & C clearance against Lug size , Therefore the Lug is is   
    ACCEPTABLE
     
Per PTS Section 6.3     
 a) Lug hole diameter, d shall be Max of     i) Dp + 3mm
    ii) Dp X 1.05
 b) Lug hole diameter, d shall be less than < (Dp + 6mm)     
  Dp = 33 result a)
     b)
    Hole,d
Diameter of hole, d  btw  31.70 33 34.70
     
No of lug eye,     
Maximum combined force acting on lug eye, Fc     
     
     
     
LIFTING LUG MATERIAL & MECHANICAL PROPERTIES     
Material used     
Specified yield stress, Sy     
Allowable bending stress, fbx.all ( = 0.66Sy ) _In Plane     
Allowable bending stress, fby.all ( = 0.75Sy ) _Out Of Plane     
Allowable tensile stress, St.all ( = 0.6Sy )     
Allowable bearing stress, Sbr.all ( = 0.9Sy )     
Allowable shear stress, Ss.all ( = 0.4Sy )     
     
SHACKLES      
Shackle rating ( S.W.L )     
Type of shackle     BOLT Type Anchor shackle G2130
Pin size, Dp     
     
MAXIMUM SLING TENSION ON PADEYE     Ts
FACTOR OF SAFETY     F.O.S.
     
DESIGN LOAD:     
SLING TENSION   P = FOS * Ts  P
LIFTING ANGLE     a
ACTUAL OUT OF PLANE ANGLE     b
VERTICAL FORCE ON PADEYE   Fz = P * sin a  Fz
OUT OF PLANE FORCE   Fyl = P * sin b  Fyl
HORIZONTAL FORCE ON PADEYE   Fx = P * cos a  Fx
Horizontal dist.PIN CL to N.A.     exl
     
STRESS CHECK AT BASE     
     
Moment Calc at distance , H     
     
In Plane Moment  My = ( Fx*H ) - ( Fz*ex l)   My
Out of plane moment   Mx = ( FyI*hL )  Mx
     
Tensile Stress     
     
Maximum tensile force, ft =  Fz / [ tL * wL ]     
Allowable tensile stress, St.all ( = 0.6Sy )     
Since ft < St.all, therefore the lug size is   satisfactory.
     
Bending stress (In Plane)     
     
Maximum bending stress , fbx =  ( 6*Mx ) / ( wL * [(tL+tcp)^2] )     
Allowable bending stress, fbx.all ( = 0.66Sy ) _In Plane     
Since fbx < fbx.all,therefore the lug size is   satisfactory.
     
Bending stress (Out of Plane)      
     
Maximum bending stress , fby =  ( 6*My ) / [ tL +(2*tcp)] * [ wL^2 ] )     
Allowable bending stress, fby.all ( = 0.75Sy ) _Out Of Plane     
Since fby < fby.all,therefore the lug size is   satisfactory.
     
     
Combined stresses,     
     
   U          = St/St.all + fby/fby.all + fbx/fbx.all    
Since U < 1, therefore the lug size is   satisfactory.
     
SHEAR stress (In Plane)      
     
Maximum SHEAR stress , fsx =  Fx / [ wL * tL ]     
Allowable shear stress, Ss.all ( = 0.4Sy )     
Since fsx < Ss.all,therefore the lug size is   satisfactory.
     
Bending stress (Out of Plane)     
     
Maximum SHEAR stress , fsy =  Fyl / [ wL * tL ]     
Allowable shear stress, Ss.all ( = 0.4Sy )     
Since fsx < Ss.all,therefore the lug size is   satisfactory.
     
CHECKING VON-MISES CRITERIA      
     
Sum of stress in X-PLANE     fx = St + fby
Sum of stress in Y-PLANE     fy = St + fbx
     
Therefore, average Shear stress      fxy =  SQRT [ (fsx^2)+(fsy^2) ]
     
Maximum Combined stress     
      Fcomb =  SQRT [ (fx^2)+(fy^2)-(fx+fy+3fxy^2) ]
Allowable combined stress : Fcomb.all ( = 0.66Sy )     
Since fsx < Ss.all,therefore the lug size is   satisfactory.
     
STRESS CHECK AT PIN HOLE     
     
Tensile Stress     
     
Maximum tensile force, P     
Cross sectional area of lug eye, At = [ 2 * ( tL* ( rL - d/2 ))] + [ 2 * ( tcp* (( Dcp/2) - d/2 ))] + [ 2 * ( tcp* (( Dcp/2) - d/2 ))]     
Tensile stress, St     
Allowable tensile stress, St.all ( = 0.6Sy )     
Since St < St.all, therefore the lug size is   satisfactory.
     
Bearing Stress     
     
Maximum bearing force, P     
Cross sectional area of lug eye, Ab  = Dp * ( tL + 2tcp )     
Bearing stress, Sbr = Fbr / Ab     
Allowable bearing stress, Sbr.all ( = 0.9Sy )     
Since Sbr  < Sbr.all,therefore the lug size is   satisfactory.
     
     
Shear Stress    `
     
Maximum shear force, P     
Cross sectional area of lug eye, At = [ 2 * ( tL* ( rL - d/2 ))] + [ 2 * ( tcp* (( Dcp/2) - d/2 ))] + [ 2 * ( tcp* (( Dcp/2) - d/2 ))]     
Shear stress, Ss     
Allowable shear stress, Ss.all ( = 0.4Sy )     
Since Ss  < Ss.all,therefore the lug size is   satisfactory.
     
Combined stresses,     
     
   U          = St/St.all + fby/fby.all + fbx/fbx.all    
Since U < 1, therefore the lug size is   satisfactory.
     
WELD SIZE CALCULATIONS     
     
Weld leg used,      
Weld throat thickness used, tr     
     
Filler metal material     
Fillet weld joint efficiency, E     
Welding stress for steel grade 43 ( E-43 ),      
Allowable welding stress,Sw     
     
Tensile Stress     
     
Maximum tensile force,Ft     
Area of weld, Aw  = 2*(tL+wL)*tr      
Tensile stress, St = [(Ft/Aw)]     
     
Since St < Sw,therefore weld leg is   satisfactory.
     
Shear stress     
     
Maximum shear force,Ft     
Shear stress, Ss = (Ft/Aw)     
Allowable welding stress for steel grade 43 ( E-43 ), Sw     
Since Ss < Sw,therefore weld leg dimension is   SATISFACTORY.
     
Bending stress     
     
Maximum bending force,Fb     
Bending stress, Sb = [(Fb/Aw)]     
Allowable welding stress for steel grade 43 ( E-43 ), Sw     

Calculation Reference
Skid Design
Structural Steel Design
Lifting Lug