Conduction
0 ContainersFiles in Conduction
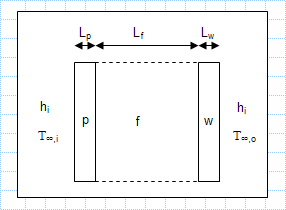
Compare thermal resistance of three walls.xls
KNOWN: Configurations of exterior wall. Inner and outer surface conditions.
FIND: Heating load for each of the three cases.
ASSUM...
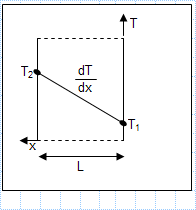
Effect of co-ordinate system on thermal gradient calculations.xls
KNOWN: Plane wall with prescribed thermal conductivity, thickness and surface temperature.
FIND: Heat flux q'x, and temperature gradie...
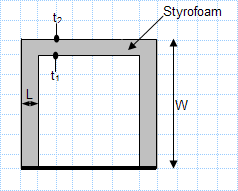
Heat loss through freezer walls by condiction.xls
KNOWN: Dimensions and thermal conductivity of food/beverage container. Inner and outer surface temperatures.
FIND: Heat flux through c...
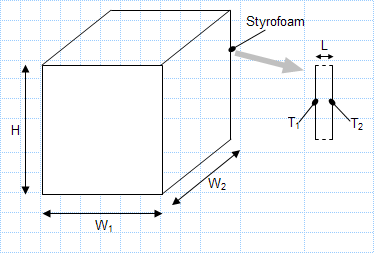
Heat loss through insulated food container.xls
KNOWN: Dimensions and thermal conductivity of food/beverage container. Inner and outer surface temperatures.
FIND: Heat flux through c...
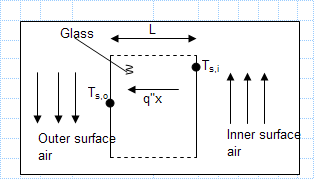
Heat loss through single glass pane.xls
KNOWN: Inner and outer surface temperatures of a glass window of prescribed dimensions.
FIND: Heat loss through window.
ASSUMPTIO...
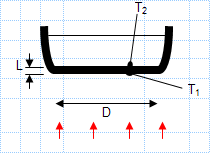
Heat transfer in a pan.xls
KNOWN: Thickness, diameter and inner surface temperature of bottom of pan used to boil water. Rate of heat transfer to pan.
FIND: Outer su...

PCB Equivalent Conductivity
Calculation of equivalent PCB thermal conductivity properties based on copper layers and copper coverage.
Calculation Reference ...
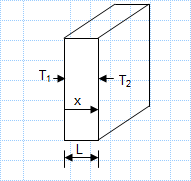
Simple 1D conduction.xls
Known: Heat rate, q, through one-dimensional wall of area A, thickness L,thermal conductivity k and inner temperature, T1. Find: The outer tem...
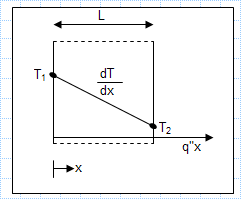
Simple 1D thermal conductivity calculations.xls
KNOWN: One-dimensional system with prescribed thermal conductivity and thickness.
FIND: Unknowns for various temperature conditions an...
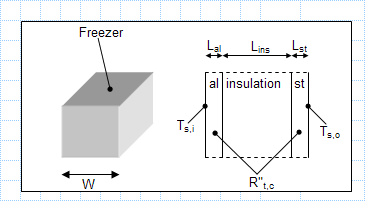
Size and surface temperature of a cubical freezer.xls
KNOWN: Size and surface temperature of a cubical freezer. Materials, thicknesses and interface resistances of freezer wall. FIND: Cooling ...
Steady state heat transfer conduction plus convection.xls
KNOWN: Inner surface temperature, thickness and thermal conductivity of insulation exposed at its outer surface to air of prescribed temper...
Thermal conductivity calculation.xls
KNOWN: Heat flux and surface temperatures associated with a slab of prescribed thickness. FIND: Thermal conductivity, k, of the wood. ASS...

