Radiation
0 ContainersFiles in Radiation
Order by
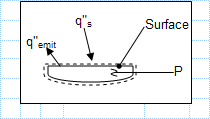
Effect of solar flux.xls
Short Description:
KNOWN: Surface area of electronic package and power dissipation by the electronics. Surface emissivity and absorptivity to solar radiation....
Submitted By:
Last Modified
24 Jan 2007
Downloads:
93
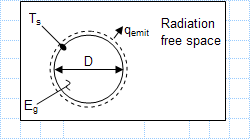
Emissivity of spherical interplanetary probe.xls
Short Description:
Known: Diameter and emissivity of spherical interplanetary probe. Power dissipation within probe. Find: robe surface temperature Assumptions:...
Submitted By:
Last Modified
24 Jan 2007
Downloads:
69
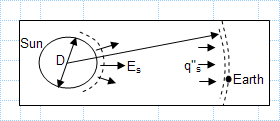
Radiation solar flux on earth.xls
Short Description:
KNOWN: Solar flux at outer edge of earth's atmosphere, 1353 W/m2.
FIND: a) Emissive power of sun.
b) Surface temperature of sun. ...
Submitted By:
Last Modified
24 Jan 2007
Downloads:
122
Surface radiation example.xls
Short Description:
Known: Area, emissivity and temperature of a surface placed in a large, evacuated chamber of prescribed temperature. Find: a) Rate of surface ...
Submitted By:
Last Modified
24 Jan 2007
Downloads:
107