Motion
0 ContainersFiles in Motion
Order by
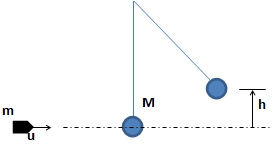
Ballistic Pendulum
Short Description:
Purpose of calculation: Ballistic Pendulum
Calculation Reference http://hyperphysics.phy-astr.gsu.edu/hbase/balpen.html#c2
C...
Submitted By:
Last Modified
06 Oct 2010
Downloads:
59
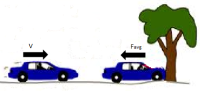
Car Crash Analysis
Short Description:
Purpose of calculation: Calculation to show the forces on a car and driver in a car crash
Calculation Reference http://hyperphysi...
Submitted By:
Last Modified
06 Oct 2010
Downloads:
152

Friction Resisting Motion
Short Description:
Purpose of calculation: Coefficient of Friction
Calculation Reference http://hyperphysics.phy-astr.gsu.edu/hbase/hpul2.html#c2 ...
Submitted By:
Last Modified
06 Oct 2010
Downloads:
70

Machinery's Handbook Motion with Constant Acceleration
Short Description:
This spreadsheet has dozens of linear and angular motion with constant acceleration equations from Machinery's Handbook 26th ...
Submitted By:
Last Modified
11 Aug 2014
Downloads:
90