Volumes
0 ContainersFiles in Volumes
Order by

Bar Cutting Form
Short Description:
Bar cutting calculator.
Calculation Reference
Reinfoced Concrete
Structural Design
Steel Designers Manual
...Submitted By:
Last Modified
20 Jun 2012
Downloads:
80
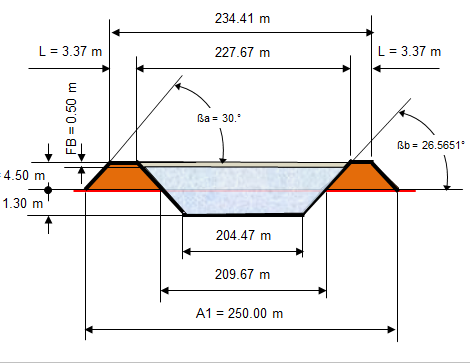
Dike with balanced volumes
Short Description:
This calculation determine the dimensions of a dike or basin and for which the volume of the excavated material is equalized with the volum...
Submitted By:
Last Modified
06 Jul 2017
Downloads:
49
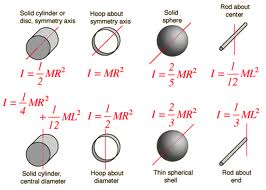
Mass Moments of Inertia
Short Description:
Purpose of calculation: Moments of Inertia
Calculation Reference http://hyperphysics.phy-astr.gsu.edu/hbase/mi.html ...
Submitted By:
Last Modified
06 Oct 2010
Downloads:
108
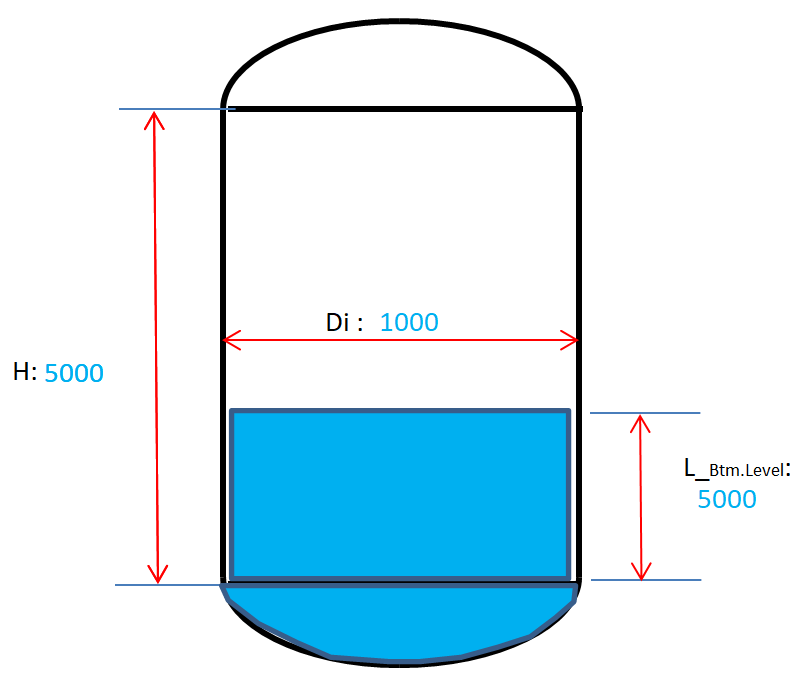
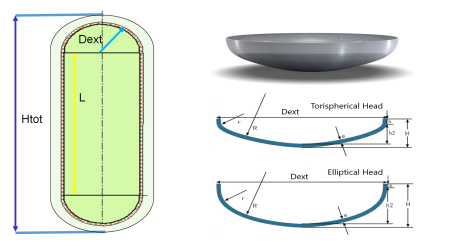
Pressure Vessel(2:1 ellipsoidal head type) Volume Calculation
Short Description:
Volume calculation for:
Horizontal pressure vessel with 2:1 ellipsoidal head type Vertical pressure vessel with 2:1 ellipsoidal head ty...
Submitted By:
Last Modified
25 Dec 2021
Downloads:
34
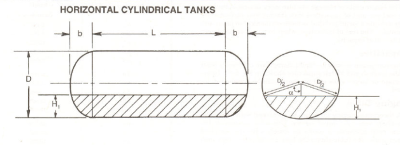
Vessels Composed of Surfaces of Revolution
Short Description:
Using the formulae for frustum of a cone, this file computes the volumes, the surfaces and the weights of plates (annular or plain), cylind...
Submitted By:
Last Modified
31 May 2013
Downloads:
80