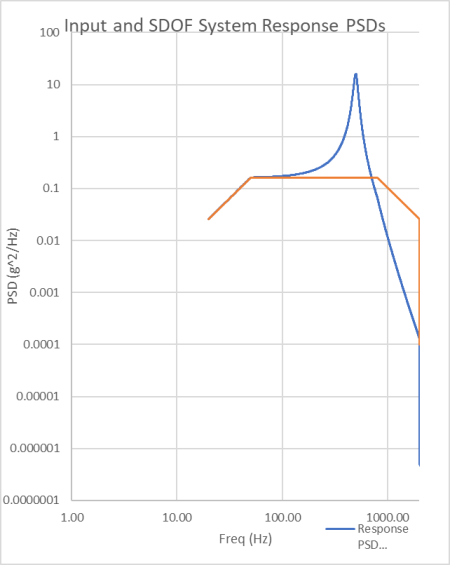
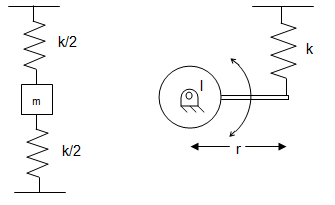
Single DOF
0 ContainersFiles in Single DOF
Order by

Centripetal Force and Acceleration.xls
Short Description:
Purpose of calculation: Centripetal Force & Acceleration
Calculation Reference http://hyperphysics.phy-astr.gsu.edu/hbase/cf.html...
Submitted By:
Last Modified
06 Oct 2010
Downloads:
71
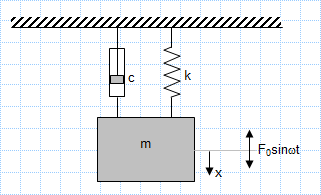
Forced Vibration of a single degree of freedom system.xls
Short Description:
Calculate an impact factor applicable to forced vibration of a single degree of freedom.
For optimum viewing double-click to...
Submitted By:
Last Modified
15 Apr 2008
Downloads:
435
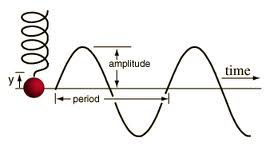
Simple Harmonic Motion
Short Description:
Purpose of calculation: Simple Harmonic Motion
Calculation Reference http://hyperphysics.phy-astr.gsu.edu/hbase/shm.html
Calc...
Submitted By:
Last Modified
06 Oct 2010
Downloads:
90
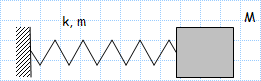
Single DOF Dynamics - Spring with attached mass.xls
Short Description:
Calculate natural frequency of coil spring with mass attached.
Calculation Reference Harris' Shock and Vibration Handbook
A sing...
Submitted By:
Last Modified
24 Jan 2007
Downloads:
620