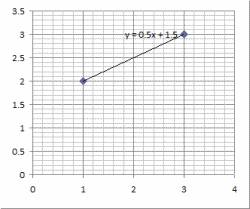
Coordinates
0 ContainersFiles in Coordinates
Andy Pope's Excel Charts
0
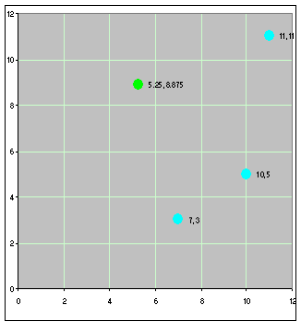
Circle through three points.xls
Let the three given points be a, b, c. Use ax and ay to represent the x and y coordinates of a, and so on. The coordinates of the center p=(px,py...
3
1
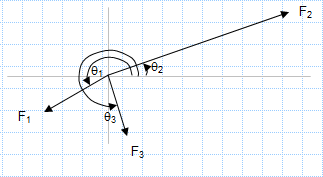
Equilibrium of three forces in a plane.xls
Purpose of calculation:
A force of known value F1 is in equilibrium with two other forces of unknown magnitude (F2 & F3).
...
1
Experiments with Parametric Sketches using XY Charts
1
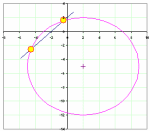
intersect_circle_line.xls
Purpose of calculation: Find points of intersection between a straight line and a circle. Note #NUM! error if there is no intersection...
1
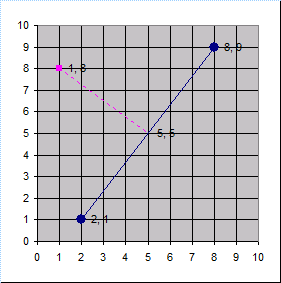
Line between two point and perpendicular distance to third point.xls
Purpose of calculation:
a) Find the equation of a line through two points.
b) Calculate the shortest dist...
3
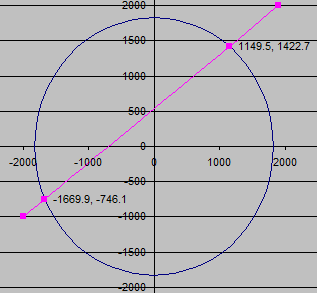
Line intersecting circle.xls
Purpose of calculation Find intersection between a line and a circle with centre at origin.
Calculation Reference Geometry for Enjoy...
1
radius of curvature
1
Straight Line Between Two Points.xls
Purpose of calculation: Find equation of a line given 2 coordinates
Calculation Reference First principles
Calculation Validat...
0
Survey point calculation
Two simple calculations included. The first is calculation of distance and bearing between two given survey points (E,N). The second is...
2
Search Repository
Submit