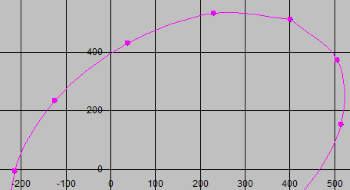
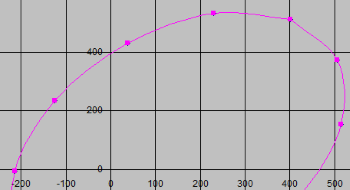
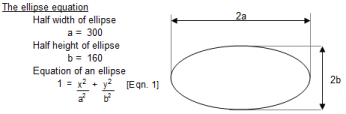
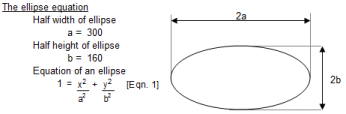
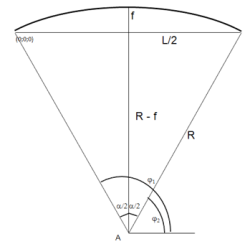
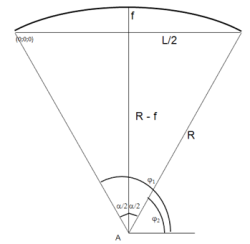
Coordinates
0 ContainersFiles in Coordinates
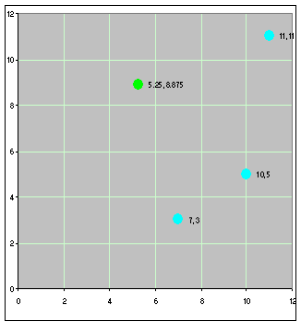
Circle through three points.xls
Let the three given points be a, b, c. Use ax and ay to represent the x and y coordinates of a, and so on. The coordinates of the center p=(px,py...
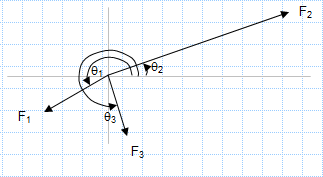
Equilibrium of three forces in a plane.xls
Purpose of calculation:
A force of known value F1 is in equilibrium with two other forces of unknown magnitude (F2 & F3).
...
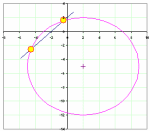
intersect_circle_line.xls
Purpose of calculation: Find points of intersection between a straight line and a circle. Note #NUM! error if there is no intersection...
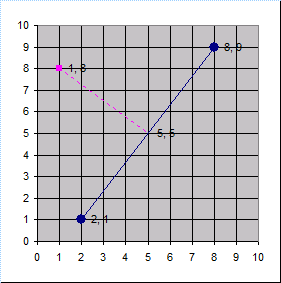
Line between two point and perpendicular distance to third point.xls
Purpose of calculation:
a) Find the equation of a line through two points.
b) Calculate the shortest dist...
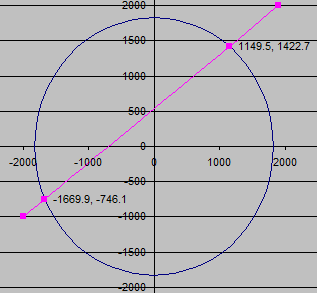
Line intersecting circle.xls
Purpose of calculation Find intersection between a line and a circle with centre at origin.
Calculation Reference Geometry for Enjoy...
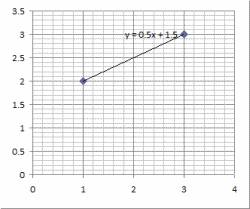
Straight Line Between Two Points.xls
Purpose of calculation: Find equation of a line given 2 coordinates
Calculation Reference First principles
Calculation Validat...
Survey point calculation
Two simple calculations included. The first is calculation of distance and bearing between two given survey points (E,N). The second is...