Stress
0 ContainersFiles in Stress
Order by

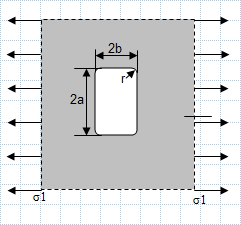
AISC360-16 RHS Welding check
Short Description:
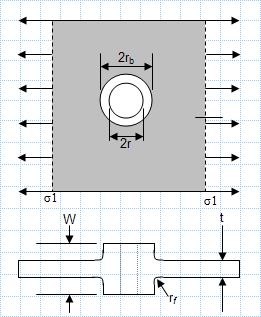
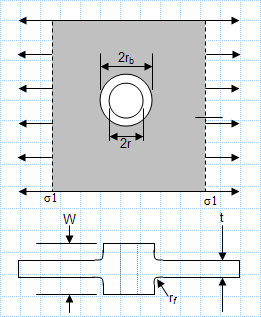
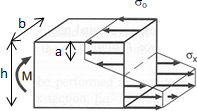
AISC360-16 RHS Welding check rev0.0The sheet calculates the weld properties A, Ix, Iy, Ip and weld stresses and compare it with AISC ...
Submitted By:
Last Modified
13 Sep 2023
Downloads:
30
Design of Prestressed Cable Systems
Short Description:
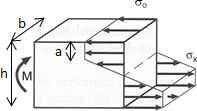
Roark's Formulas for Stress and Strain along with the use of POST-TENSIONING INSTITUTE: Issue 14.
...Submitted By:
Last Modified
27 Feb 2023
Downloads:
21
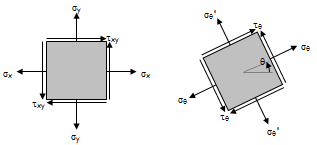
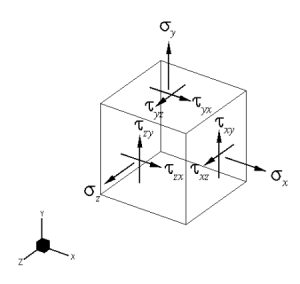
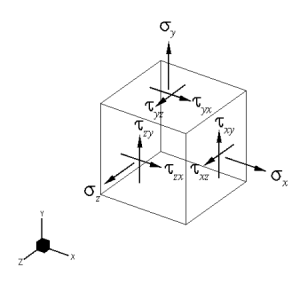
Principal Stress Calcs
Short Description:
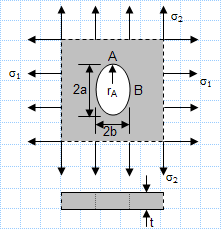
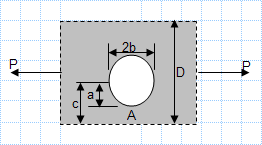
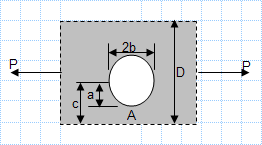
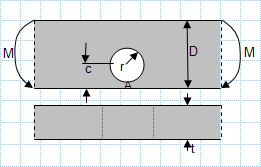
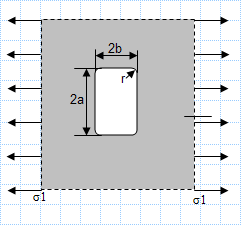
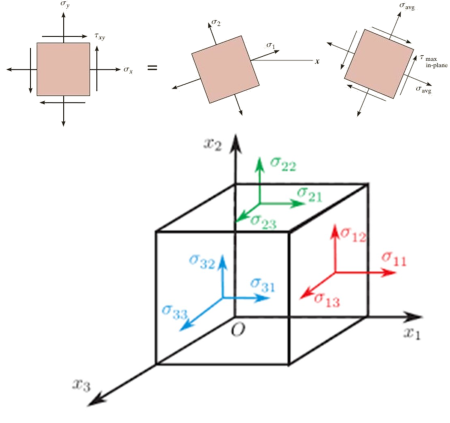
This spreadsheet calculates the various states of stress given a set of the six stress components. The three principal stresses are calculated alo...
Submitted By:
Last Modified
09 Sep 2021
Downloads:
29