Piping
0 ContainersFiles in Piping
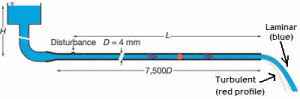
AirFlow
Calculates the Moody friction factor and then the head loss and pressure drop per classic equations.
Enter temper...

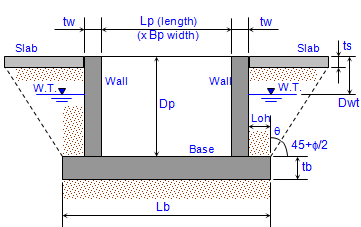
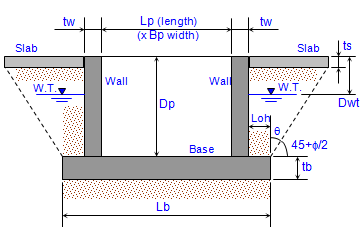
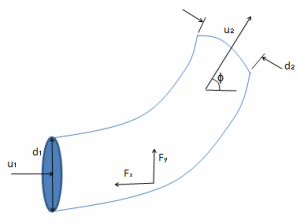
ASME CALCULATION FOR MITER BEND
Calculation Reference
ASME
Piping Design
Piping Design Codes
The American Society of Mechanical Engineers (AS...
Buoyancy control analysis
CALCULATION FOR SET ON WEIGHT Pipe size Outside diameter, OD Wall thickness, t Weight of pipe, WP Density of water, r Buoya...
Colebrook_White.xls
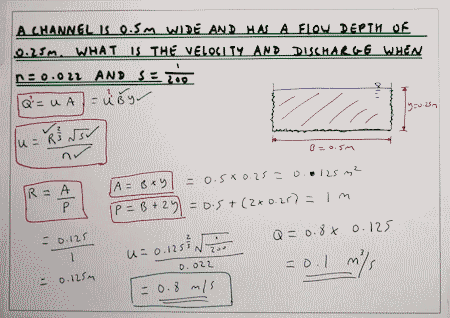
Purpose of calculation: To determine the Velocity & Flow of water through pipes of varying diameter, slope & material. Calculation Reference:...

DKE_PipingVibration_MainLines.xlsx
EI Guidelines for the Avoidance of Vibration - TM-01 Qualitative Assessment
Energy Institute Guideline...
Pipe flow/friction factor calculations
Calculation of Head Loss and Frictional Pressure Drop for given flow rate, pipe diameter, pipe length, pipe roughness, fluid density & viscosity, ...

PIPESPANS V1
PIPESPANS is a spreadsheet program written to determine the maximum stress and deflection of a pipe. Stress and deflection are calculated as funct...

PSV relief sizing
This spreadsheet calculates the required effective discharge area of a pressure safety valve. To calculate the required effective disc...

Recommended Span Length
This spreadsheet is calculating recommended pipe support spacing for piping systems - essentially determining how far apart you can place pipe supp...

Thermal Expansion
This sheet is a very simple and quick way to calculate linear thermal expansion in typical metal piping materials. Also valid for non-piping compon...

Vibration within piping downstream of high pressure cut control valves and regulators
This one calculates and assess vibration within piping downstream of high pressure cut control valves and regulators and then recomme...

Wall Thickness Calc
Pipe wall thickness calc according to
Calculation Reference Subsea Piping
Offshore Pipes
API RP 1111
API RP 1111...
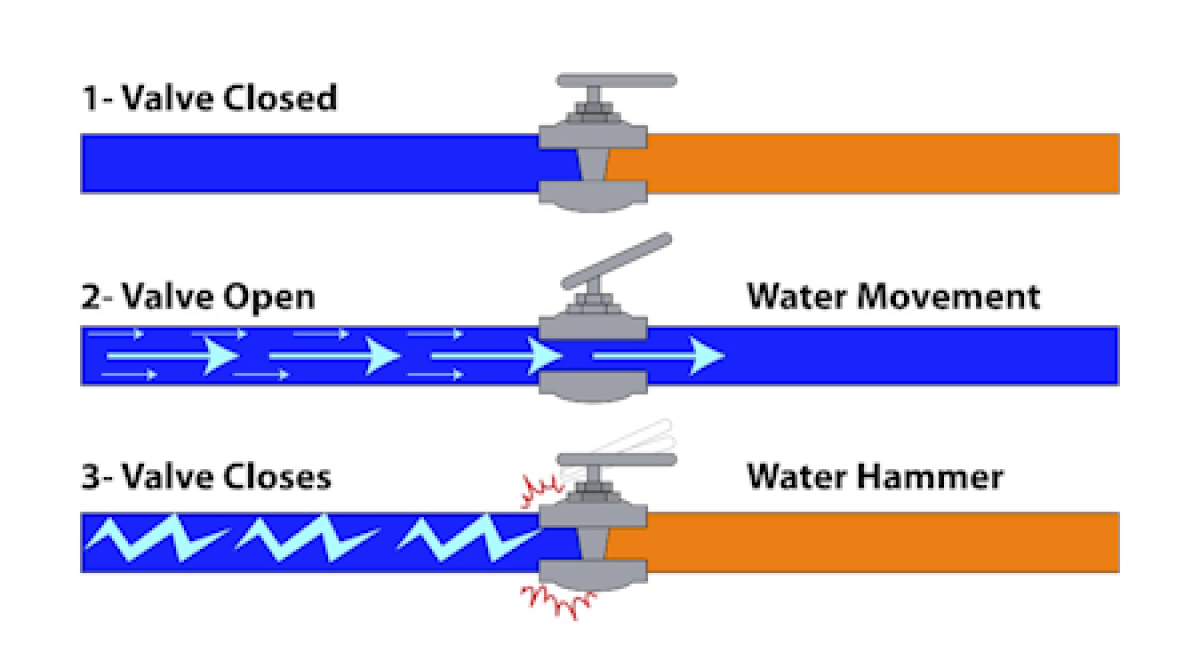
Water Hammer Pressure Calculator
Water hammer is a fluid mechanics phenomenon that occurs in piping systems when the flow of liquid is suddenly stopped or changed direction. This c...