Fluid Mechanics
0 ContainersFiles in Fluid Mechanics
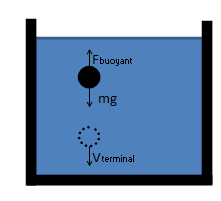
Buoyancy and Drag
Purpose of calculation: Buoyancy and drag
Calculation Reference http://hyperphysics.phy-astr.gsu.edu/hbase/lindrg.html
Calcul...

Calculate Drag Force When a Fluid Flows Around a Given Shape.xlsx
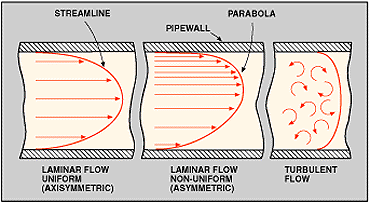
In fluid dynamics, the drag coefficient is a dimensionless quantity that is used to quantify the drag or resistance of an object in a fluid...

Complete Water Supply Treatment Plant
A Complete Water Supply Treatment Plant is a facility that treats raw water from a source (such as a ri...

COMPRESSED AIR SYSTEM
The compressed air system sizing calculation involves calculating the compressor FAD (free air...
Constant rate filtration
Constant rate filtration from https://www.particles.org.uk/filtration/
https://youtu.be/JntFJzX7dhA Constant rate filtration is a com...
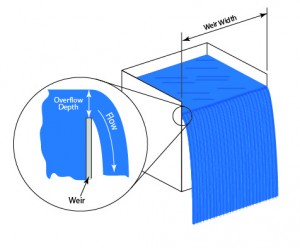
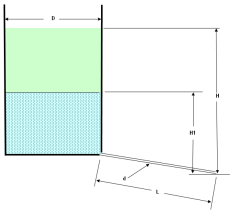
Discharge flow from an upward Pipe (uniform weir or jet)
This file determines the following parameters for two kinds of flow occurence from the end of a vertical pipe:
A) Ci...

Flare Burning Combustion Calculation
-
Input Fuel characteristics
-
Input kiln production data
-
Determine (goal seek) transport air flow rate ...

Gravity Dam Stability Analysis
SHAH-WA-ARUA MULTIPURPOSE PROJECT Gravity dam Stability Analysis:(Block-8)
The stability analysis of Non-ov...

HYDRAULIC DESIGN OF TRAJECTORY BUCKET TYPE ENERGY DISSIPATOR
HYDRAULIC DESIGN OF TRAJECTORY BUCKET TYPE ENERGY DISSIPATOR
The design is based on IS 7365:1985.
- Salient levels:
...

Limit State Box Culvert Design IRC:6-1966
Standard IRC:6-1966
1.0 Design Data
1.1 Dimension Detail
No of cells ...
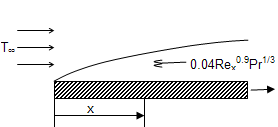
Surface shear stress in parallel flow over a flat plate.xls
KNOWN: Heat Transfer correlation associated with parallel flow over a rough flat plate Velocity and temperature of air flow over the plate....