Areas
0 ContainersFiles in Areas
Order by
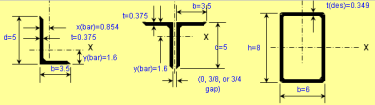
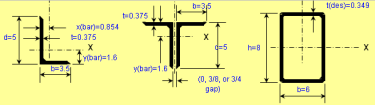
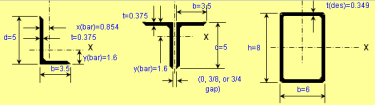
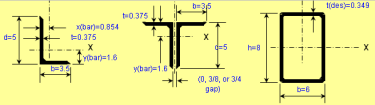
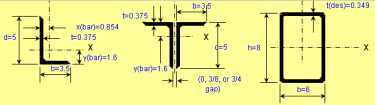
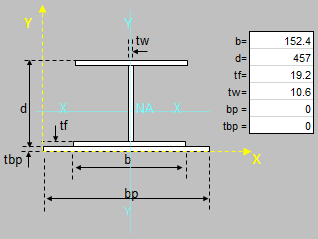
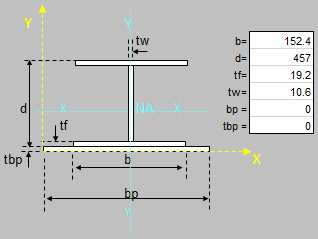
Beam/Column and Beam+Column Section Classes per AISC 360 and CSA S16
Short Description:
As you know, the calculations for beams, columns and beams plus columns are based on different equations per AISC 360 and CSA S16. These two worksh...
Submitted By:
Last Modified
19 Apr 2021
Downloads:
63

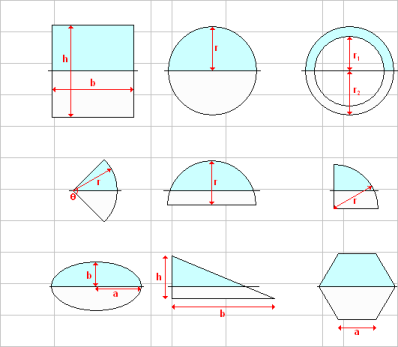
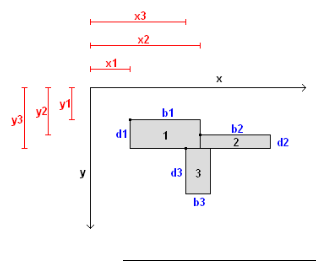
General Section Properties & Stresses
Short Description:
This spreadsheet calculates the section properties of a general shape defined by nodal co-ordinates together with the stress ...
Submitted By:
Last Modified
28 Jul 2014
Downloads:
158
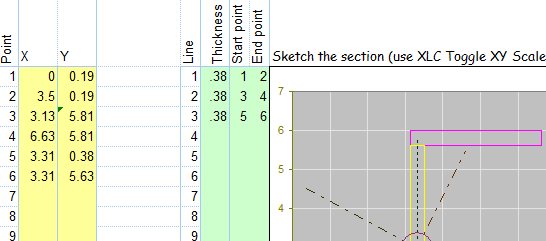
LineSec.xls
Short Description:
'LINESEC' - SECTION PROPERTY CALCULATION FOR SECTIONS DEFINED BY LINES
Program Description: 'LI...
Submitted By:
Last Modified
31 May 2011
Downloads:
207

pipe strength base on API 5L
Short Description:
Calculate pipe strength in two ways: stress and force,base API 21th wsd.
Calculation Reference
Pipe Design
Secti...
Submitted By:
Last Modified
24 Sep 2013
Downloads:
92