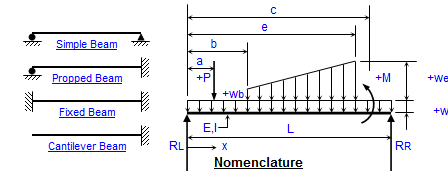
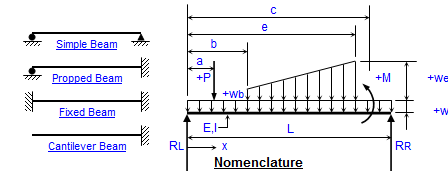
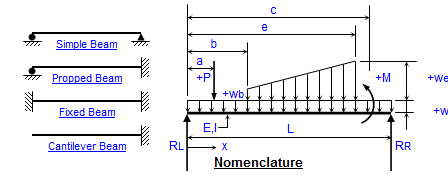
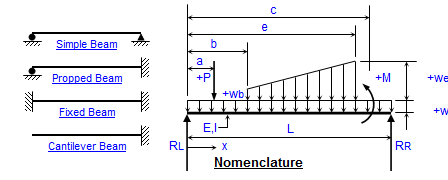
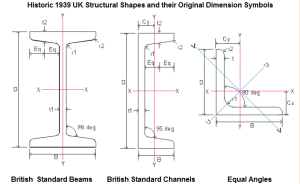
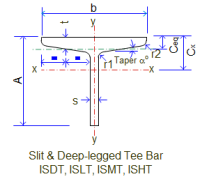
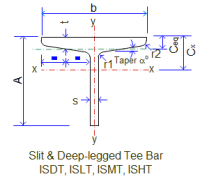
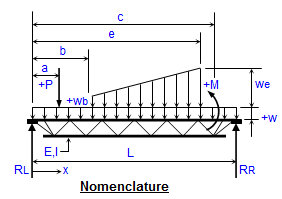
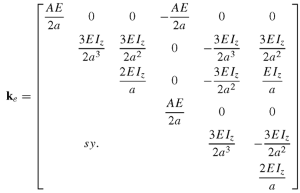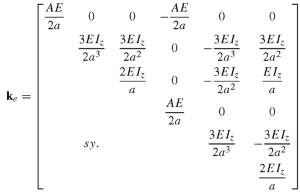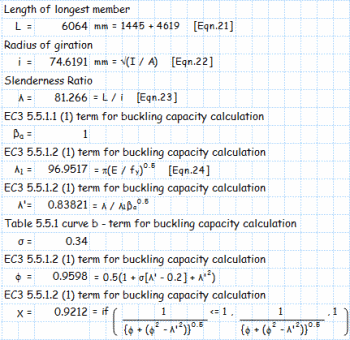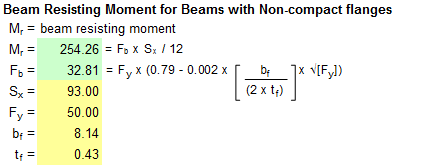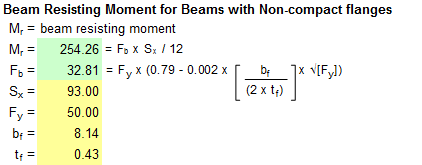Beams
0 ContainersFiles in Beams
Order by
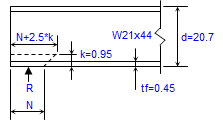
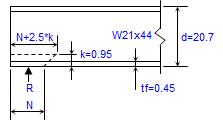
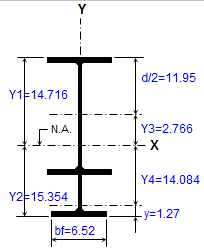
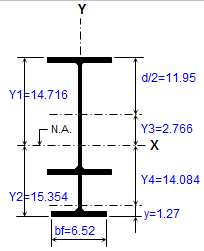
ANALYSIS & DESIGN OF RC BEAM AS PER ACI 318-08
Short Description:
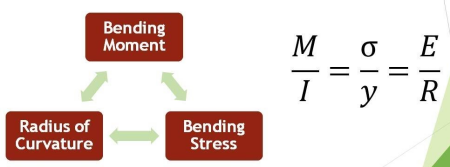
The Basic Concept: When a concrete beam bends under load, the concrete on one side gets compressed while the other side gets stretched (tension). S...
Submitted By:
Last Modified
06 Aug 2020
Downloads:
4
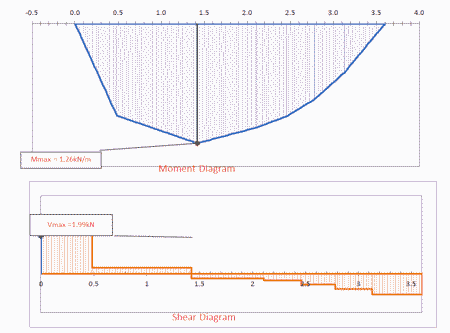
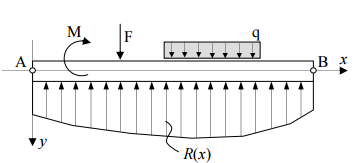
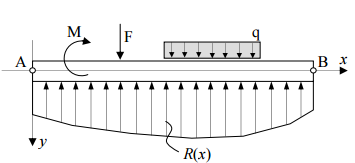
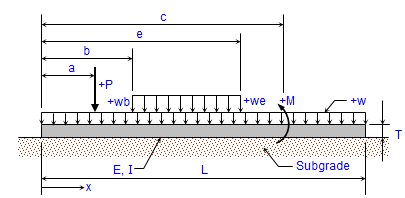
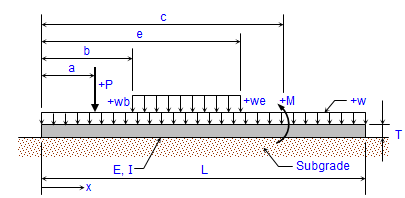
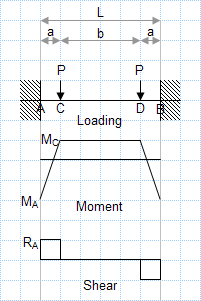
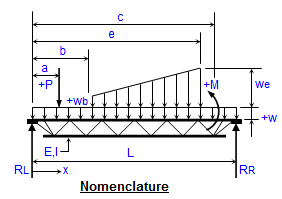
Equialent UDL from Point Loads in Beam
Short Description:
Calculating the equivalent distributed load from a set of point loads in a beam can be highly beneficial to an engineer for several reasons...
Submitted By:
Last Modified
13 Mar 2024
Downloads:
19
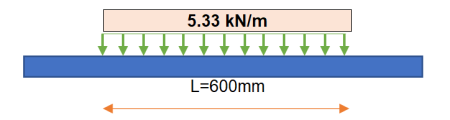
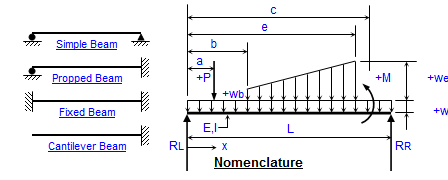
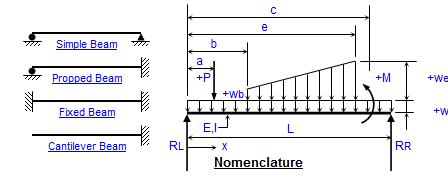
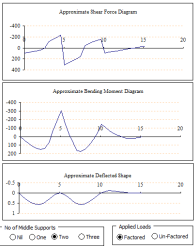
Loading Calculation Sheet.xlsx
Short Description:
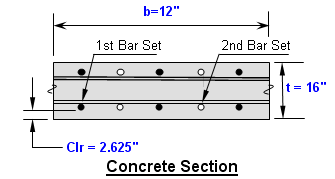
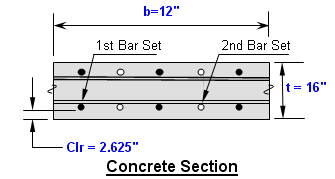
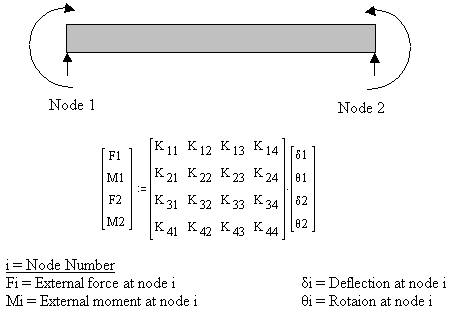
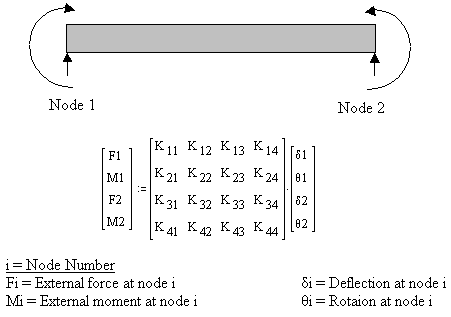
Beam bending theory is a fundamental concept in structural engineering and solid mechanics that deals with the deformation and stress distr...
Submitted By:
Last Modified
02 Jan 2023
Downloads:
19